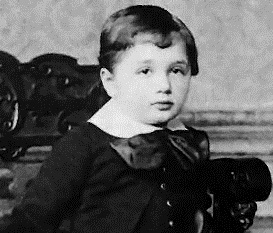Réseaux de Neurones et Apprentissage Profond
A propos des exercices et problèmes
 Utiliser des réseaux de neurones pour reconnaître des chiffres manuscrits
Utiliser des réseaux de neurones pour reconnaître des chiffres manuscrits
 Comment fonctionne l'algorithme de rétropropagation du gradient
Comment fonctionne l'algorithme de rétropropagation du gradient
 Améliorer la façon dont les réseaux de neurones apprennent
Améliorer la façon dont les réseaux de neurones apprennent
 Une preuve visuelle que les réseaux de neurones peuvent calculer n'importe quelle fonction
Une preuve visuelle que les réseaux de neurones peuvent calculer n'importe quelle fonction
 Pourquoi les réseaux de neurones profonds sont-ils difficiles à entraîner?
Pourquoi les réseaux de neurones profonds sont-ils difficiles à entraîner?
Appendice: Existe-t-il un algorithme simple pour l'intelligence?





Le système visuel humain est l'une des merveilles du monde. Considérons la séquence de chiffres manuscrits suivante :
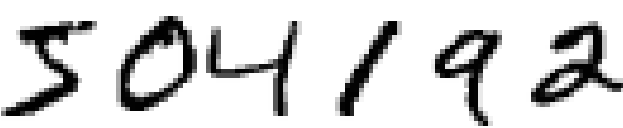
La plupart des gens reconnaissent sans effort les chiffres 504192. Cette facilité est trompeuse. Dans chaque hémisphère de notre cerveau, nous les humains possédons un cortex visuel primaire, aussi appelé V1, qui contient 140 millions de neurones reliés entre eux par des dizaines de milliards de connexions. Et pourtant la vision humaine ne met pas en jeu seulement V1, mais toute une série de cortex visuels - V2, V3, V4 et V5 - qui effectuent un traitement d'image de plus en plus complexe. Nous transportons dans nos têtes un super-ordinateur, qui a été mis au point par l'évolution pendant des centaines de millions d'années, et qui s'est adapté d'une superbe façon afin d'appréhender le monde visuel. Reconnaître des chiffres manuscrits n'est pas une chose facile. Ou plutôt, nous les humains sommes prodigieusement et incroyablement bons pour comprendre ce que nos yeux nous montrent. Mais presque tout ce travail est réalisé de façon inconsciente. C'est ce qui fait que nous ne sommes généralement pas capables d'apprécier combien le problème résolu par notre système visuel est difficile.
La difficulté de la reconnaissance visuelle devient claire si vous essayez d'écrire un programme informatique qui reconnaîtrait les chiffres tels que ceux représentés plus haut. Ce qui semble facile lorsque nous le réalisons nous-mêmes devient soudain extrêmement difficile. Des intuitions simples sur la façon dont nous reconnaissons les formes - "un 9 est formé d'une boucle en haut et d'un trait vertical en bas à droite" - s'avèrent assez compliquées à traduire en algorithme. Si vous essayez de rendre ce genre de règles plus précises, vous vous retrouvez rapidement perdu dans un bourbier d'exceptions et de cas particuliers. Cela semble sans espoir.
Les réseaux de neurones abordent le problème d'une façon différente. L'idée est de partir d'un grand nombre de chiffres manuscrits, appelés les exemples d'entrainement,

puis de développer un système capable d'apprendre à partir de ces exemples d'entrainement. Autrement dit, le réseau de neurones utilise les exemples pour inférer automatiquement des règles lui permettant de reconnaître les chiffres manuscrits. De plus, en augmentant le nombre d'exemples d'entrainement, le réseau peut en apprendre plus au sujet des caractères manuscrits, et donc améliorer sa précision. Ainsi, alors que je n'ai montré que 100 chiffres d'entrainement ci-dessus, nous pourrions peut-être construire un meilleur identifieur de caractères en utilisant des milliers ou même des millions ou des milliards d'exemples d'entrainement.
Dans ce chapitre, nous allons écrire un programme informatique qui implémente un réseau de neurones qui apprend à reconnaître des chiffres manuscrits. Le programme n'est constitué que de 74 lignes de code, et n'utilise pas de bibliothèque spécialisée dans les réseaux de neurones. Mais ce petit programme est capable de reconnaître les chiffres avec une précision de plus de 96 pour cent, et cela sans intervention humaine. Mieux encore, dans les chapitres suivants, nous développerons des idées qui permettent d'améliorer la précision pour la porter à plus de 99 pour cent. En réalité, les meilleurs réseaux de neurones du commerce sont aujourd'hui tellement bons qu'ils sont utilisés par les banques pour traiter les chèques, et par les bureaux de poste pour reconnaître les adresses.
Nous nous focalisons sur la reconnaissance de caractères manuscrits parce qu'il s'agit d'un excellent problème type pour en apprendre davantage sur les réseaux de neurones. Ce problème type permet de trouver le juste équilibre: il est stimulant - ce n'est pas rien de reconnaître des chiffres manuscrits - mais il n'est pas difficile au point de nécessiter une solution extrêmement compliquée ou une puissance de calcul extraordinaire. C'est aussi un bon moyen de développer des techniques plus avancées, telles que l'apprentissage profond. Ainsi, au cours du livre, nous reviendrons à plusieurs reprises sur le problème de la reconnaissance de caractères manuscrits. Plus loin dans le livre, nous discuterons de la manière dont ces idées peuvent être appliquées à d'autres domaines de la vision par ordinateur, et aussi à la reconnaissance vocale, au traitement du langage naturel ainsi qu'à d'autres domaines.
Bien sûr, si le seul but de ce chapitre avait été d'écrire un programme informatique capable de reconnaître des chiffres manuscrits, alors ce chapitre aurait été beaucoup plus court! Mais en cours de route, nous allons développer de nombreuses idées clés au sujet des réseaux de neurones, notamment deux types importants de neurones artificiels (le perceptron et le neurone sigmoïde), et l'algorithme d'apprentissage standard pour les réseaux de neurones, connu sous le nom de descente de gradient stochastique. Chemin faisant, je m'efforcerai d'expliquer pourquoi les choses sont faites de cette façon, et de vous rendre les réseaux de neurones intuitifs. Ceci requiert une discussion plus longue que si j'avais simplement présenté les mécanismes de base, mais cela en vaut la peine car cela vous amènera à une compréhension plus approfondie. Entre autres avantages, à la fin de ce chapitre, nous serons en mesure de comprendre ce qu'est l'apprentissage profond, et pourquoi il est important.
Les perceptrons
Qu'est-ce qu'une réseau de neurones? Pour commencer, je vais présenter un type particulier de neurone artificiel que l'on appelle un perceptron. Les perceptrons ont été développés dans les années 1950 et 1960 par le scientifique Frank Rosenblatt, inspiré par le travail de Warren McCulloch et Walter Pitts. Aujourd'hui, il est plus habituel d'utiliser d'autres modèles de neurones artificiels - dans ce livre, et dans la plupart des travaux modernes sur les réseaux de neurones, le modèle principal de neurone utilisé est celui que l'on appelle le neurone sigmoïde. Nous en arriverons aux neurones sigmoïdes bientôt. Mais pour bien comprendre pourquoi les neurones sigmoïdes ont été conçus ainsi, cela vaut la peine de prendre le temps d'étudier d'abord les perceptrons.
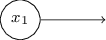
Ainsi, comment les perceptrons fonctionnent-ils? Un perceptron comprend plusieurs entrées (inputs) binaires, $x_1, x_2, \ldots$, et produit une unique valeur binaire en sortie (output):
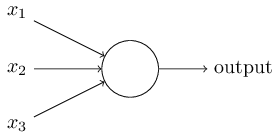
Ceci est le modèle mathématique de base. On peut voir le perceptron comme un appareil qui prend des décisions en soupesant les données. Laissez-moi donner un exemple. Ce n'est pas un exemple très réaliste, mais il est facile à comprendre, et nous en viendrons bientôt à des exemples plus réalistes. Supposons que le week end arrive, et que vous ayez entendu qu'il va y avoir un festival du fromage dans votre ville. Vous aimez le fromage, et vous essayez de décider si vous allez vous rendre à ce festival ou non. Vous pourriez prendre votre décision en considérant trois facteurs:
- Est-ce qu'il fait beau?
- Est-ce que votre ami ou votre amie veut bien vous accompagner?
- Le festival est-il accessible par les transports en commun? (Vous n'avez pas de voiture).
Maintenant, supposons que vous adorez vraiment le fromage, à tel point que vous seriez partant pour vous rendre au festival même si votre ami ou amie n'est pas intéressé et qu'il est difficile de s'y rendre. Mais peut-être détestez vraiment le mauvais temps et il est hors de question d'aller au festival en cas de mauvais temps. Vous pouvez utiliser des perceptrons pour modéliser ce genre de prise de décision. Une façon de faire est de choisir un poids $w_1 = 6$ pour la météo, et $w_2 = 2$ et $w_3 = 2$ pour les autres conditions. La valeur de $w_1$ plus grande que les autres indique que la météo est un facteur important pour vous, beaucoup plus que le fait que votre ami ou amie vienne avec vous, ou la proximité des transports en commun. Finalement, supposons que vous choisissiez un seuil de $5$ pour le perceptron. Avec ces choix, le perceptron implémente le modèle de prise de décision souhaité, et renvoie la valeur $1$ s'il fait beau, et $0$ si la météo est mauvaise. La sortie reste la même que votre ami ou amie souhaite venir ou non, ou qu'il y ait la possibilité d'utiliser les transports en commun ou non.
En faisant varier les poids et le seuil, nous pouvons obtenir d'autres modèles de prise de décision. Par exemple, supposons que l'on ait choisi plutôt un seuil de $3$. Alors le perceptron déciderait que vous devriez vous rendre au festival s'il fait beau, ou si le festival est desservi par les transports en commun et votre ami ou amie souhaite vous accompagner. En d'autres termes, il s'agirait d'un modèle de prise de décision différent. Faire diminuer le seuil signifie que vous avez une plus grande envie de vous rendre au festival.
Evidemment, le perceptron n'est pas une modélisation complète du système de prise de décision humain! Mais l'exemple permet d'illustrer comment un perceptron est capable de soupeser différents types d'information afin de construire des décisions. Et il devrait aller de soi qu'un réseau complexe de perceptrons serait capable de prendre des décisions assez subtiles:
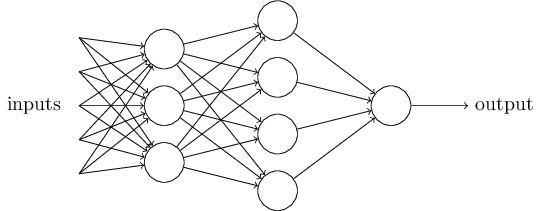
Au passage, quand j'ai défini les perceptrons, j'ai dit qu'un perceptron ne possédait qu'une seule sortie. Dans le réseau ci-dessus, il semblerait que les perceptrons possèdent plusieurs sorties. En réalité, ils n'ont toujours qu'une seule sortie. Les multiples flèches de sortie sont simplement un moyen pratique pour indiquer que la sortie d'un perceptron est utilisée comme entrée pour plusieurs autres perceptrons. C'est plus simple que de dessiner une sortie unique qui se diviserait par la suite.
Simplifions la façon dont nous décrivons les perceptrons. La condition $\sum_j w_j x_j > \mbox{seuil}$ est lourde, et nous pouvons effectuer deux changements de notation pour la simplifier. Le premier changement consiste à écrire $\sum_j w_j x_j$ comme un produit scalaire, $w \cdot x \equiv \sum_j w_j x_j$, où $w$ et $x$ sont des vecteurs dont les composantes sont respectivement les poids et les entrées. Le second changement consiste à transférer le seuil de l'autre côté de l'inégalité, et de le remplacer par ce qui est appelé le biais du perceptron, $b \equiv -\mbox{seuil}$. Si l'on utilise le biais à la place du seuil, la règle du perceptron se réécrit: \begin{eqnarray} \mbox{sortie} = \left\{ \begin{array}{ll} 0 & \mbox{if } w\cdot x + b \leq 0 \\ 1 & \mbox{if } w\cdot x + b > 0 \end{array} \right. \tag{2}\end{eqnarray} Vous pouvez voir le biais comme une mesure de la facilité avec laquelle le perceptron va produire un $1$ en sortie. Ou pour l'exprimer en termes plus biologiques, le biais est une mesure de la propension du perceptron à se déclencher. Pour un perceptron avec un très gros biais, il est extrêmement facile pour le perceptron de produire un $1$. Mais si le biais est très négatif, alors il est difficile pour le perceptron de produire un $1$. Evidemment, l'introduction du biais n'est qu'un changement mineur dans notre description des perceptrons, mais nous verrons plus loin que cela nous conduira à d'autres simplifications dans les notations. Pour cette raison, dans le reste du livre, nous n'utiliserons plus le seuil, nous utiliserons toujours le biais.
J'ai décrit les perceptrons comme étant une méthode pour soupeser les
informations afin de fabriquer des décisions.
Une autre façon d'utiliser les perceptrons est de leur faire calculer
les fonctions logiques élémentaires que l'on considère habituellement
comme étant sous-jacentes au calcul, des fonctions telles que
ET, OU, et NON-ET.
Supposons par exemple que nous ayons un perceptron avec deux entrées,
chacune avec un poids $-2$, et avec un biais global de $3$.
Voici notre perceptron :
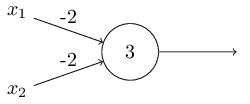
NON-ET!
L'exemple de la porte NON-ET montre que nous pouvons
utiliser les perceptrons pour calculer des fonctions logiques simples.
En fait, nous pouvons utiliser des réseaux de perceptrons pour calculer toutes
les fonctions logiques que l'on veut.
Ceci provient du fait que la porte NON-ET est universelle
pour le calcul logique, c'est-à-dire que nous pouvons construire tout calcul
en assemblant des portes NON-ET.
Par exemple, nous pouvons utiliser des portes NON-ET pour construire
un circuit qui additionne deux bits, $x_1$ et $x_2$.
Ceci nécessite de calculer la somme bit à bit, $x_1 \oplus x_2$,
ainsi qu'un bit de retenue (carry bit) qui est mis à $1$ lorsqu'à la fois $x_1$ et $x_2$ valent $1$,
c'est-à-dire que le bit de retenue est simplement le produit bit à bit $x_1 x_2$:
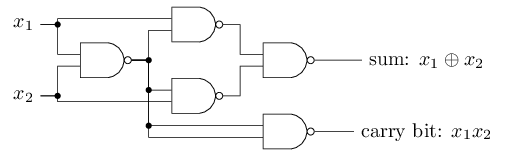
NON-ET par des perceptrons à deux entrées,
chacune avec un poids $-2$, et un biais global de $3$. Voici le réseau obtenu.
Vous pouvez remarquer que j'ai un peu déplacé le perceptron correspondant
à la porte NON-ET située en bas à droite, simplement pour faciliter
le dessin des flèches sur le diagramme:
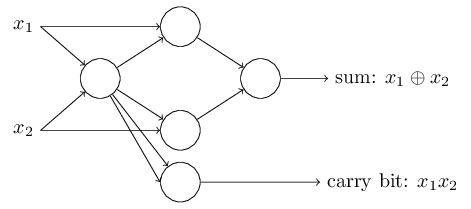
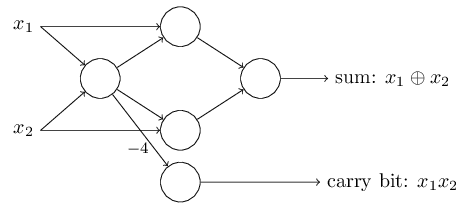
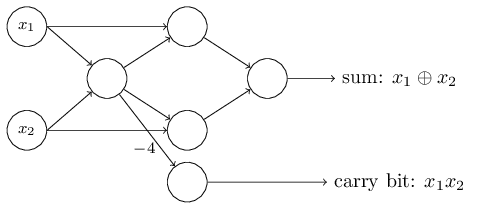
L'exemple de l'additionneur montre comment un réseau de perceptrons peut
être utilisé pour simuler un circuit qui contient de nombreuses portes
NON-ET.
Et comme les portes NON-ET sont universelles pour le calcul
logique, il s'ensuit que les perceptrons sont eux aussi universels pour le
calcul.
L'universalité des perceptrons pour le calcul est à la fois
rassurante et décevante. Elle est rassurante car elle nous dit
que les réseaux de perceptrons peuvent être aussi puissants que
n'importe quel autre outil de calcul. Mais elle est aussi décevante
parce qu'elle semble signifier que les perceptrons sont seulement
un nouveau type de porte NON-ET.
Il n'y a rien de révolutionnaire!
Cependant, la situation est meilleure qu'il n'y paraît.
Il se trouve que nous pouvons concevoir des algorithmes d'apprentissage
capables de régler automatiquement les poids et les biais d'un réseau de neurones
artificiels. Ces réglages se produisent en réponse à des stimuli,
sans intervention directe du programmeur. Ces algorithmes d'apprentissage nous
permettent d'utiliser les neurones artificiels d'une façon radicalement différente
des portes logiques conventionnelles. Au lieu de disposer explicitement un circuit
de portes NON-ET et d'autres portes, notre réseau de neurones
peut apprendre de façon simple à résoudre des problèmes pour lesquels il
serait extrêmement difficile de concevoir directement un circuit conventionnel.
Les neurones sigmoïdes
Les algorithmes d'apprentissage semblent fantastiques. Mais comment pouvons-nous concevoir de tels algorithmes pour un réseau de neurones? Supposons que nous ayons un réseau de perceptrons que nous souhaiterions utiliser pour apprendre à résoudre un problème. Par exemple, les entrées du réseau pourraient être les données des pixels bruts obtenus à partir d'une image scannée d'un chiffre manuscrit. Et nous souhaiterions que le réseau apprenne les poids et les biais de sorte que la sortie du réseau classifie correctement le chiffre. Pour voir comment fonctionne l'apprentissage, supposons que nous effectuions une petite modification sur un des poids (ou biais) du réseau. Ce que nous souhaiterions, c'est qu'une petite modification sur un des poids occasionne seulement un petit changement sur la sortie du réseau. Comme nous le verrons bientôt, c'est cette propriété qui va rendre l'apprentissage possible. Schématiquement, voici ce que nous voulons (évidemment ce réseau est trop simple pour faire de la reconnaissance de caractères manuscrits!) :
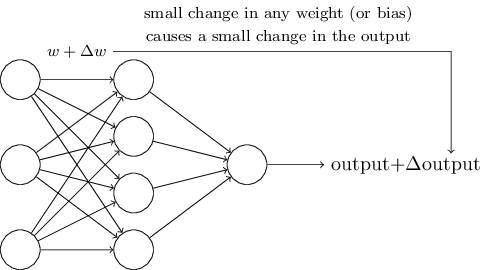
S'il était vrai qu'une petite modification sur un poids (ou un biais) occasionne seulement une petite modification sur la sortie, alors nous pourrions exploiter ce fait pour modifier les poids et les biais afin que notre réseau se comporte un peu plus de la manière dont on voudrait qu'il se comporte. Par exemple, supposons que le réseau ait classifié par erreur une image comme étant un "8" alors qu'il aurait dû répondre "9". Nous pourrions envisager comment effectuer une petite modification dans les poids et les biais de sorte que le réseau se rapproche un petit peu d'un état dans lequel il classifierait l'image comme étant un "9". Et ensuite nous répéterions cela, en changeant continuellement les poids et les biais pour produire des sorties toujours meilleures. Le réseau serait en train d'apprendre.
Le problème est que ce n'est pas ainsi que les choses vont se passer lorsque notre réseau contient des perceptrons. En réalité, un petit changement dans les poids ou les biais de n'importe quel perceptron dans le réseau peut parfois complètement inverser la sortie du perceptron, disons de $0$ à $1$. Cette inversion peut alors conduire à modifier complètement le comportement du réseau, d'une façon très compliquée. Ainsi, tandis que notre "9" pourrait bien être classifié correctement maintenant, le comportement du réseau sur toutes les autres images serait probablement complètement modifié, et ce d'une manière difficile à contrôler. Ceci rend difficile de voir comment modifier de façon progressive les poids et les biais de sorte que réseau se rapproche du comportement souhaité. Peut-être qu'il existe un moyen intelligent de régler ce problème. Mais ce n'est pas du tout évident de voir comment faire en sorte qu'un réseau de perceptrons apprenne.
Nous pouvons résoudre ce problème en introduisant un nouveau type de neurone artificiel appelé un neurone sigmoïde. Les neurones sigmoïdes ressemblent aux perceptrons, mais sont modifiés de sorte que des petits changements dans leurs poids et leur biais provoquent seulement un petit changement dans leur sortie. Il s'agit du point crucial qui permettra au réseau de neurones sigmoïdes d'apprendre.
D'accord, laissez-moi décrire le neurone sigmoïde. Nous dessinerons les neurones sigmoïdes de la même façon que les perceptrons:
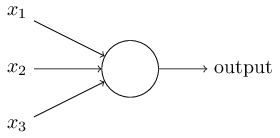
A première vue, les neurones sigmoïdes semblent très différents des perceptrons. La forme algébrique de la fonction sigmoïde peut sembler opaque et austère si vous n'êtes pas déjà familier avec elle. En réalité, il existe de nombreuses similitudes entre les perceptrons et les neurones sigmoïdes, et il s'avère que la forme algébrique de la fonction sigmoïde est plus un détail technique qu'un véritable obstacle à la compréhension.
Pour comprendre la similarité avec le modèle du perceptron, supposons que $z \equiv w \cdot x + b$ soit un grand nombre positif. Alors $e^{-z} \approx 0$ et ainsi $\sigma(z) \approx 1$. Autrement dit, lorsque $z = w \cdot x+b$ est grand et positif, la sortie du neurone sigmoïde vaut approximativement $1$, exactement comme cela aurait été le cas pour un perceptron. D'un autre côté, supposons que $z = w \cdot x+b$ soit très négatif. Alors $e^{-z} \rightarrow \infty$, et $\sigma(z) \approx 0$. Ainsi lorsque $z = w \cdot x +b$ est très négatif, le comportement du neurone sigmoïde est de nouveau une bonne approximation du perceptron. C'est seulement lorsque $w \cdot x+b$ est de taille modeste que l'on observe beaucoup plus d'écart avec le modèle du perceptron.
Que peut-on dire de la forme algébrique de $\sigma$? Comment pouvons-nous la comprendre? En fait, la forme exacte de $\sigma$ n'est pas si importante - ce qui compte réellement est la forme de la courbe de la fonction lorsqu'on la trace. Voici la forme de la courbe:
Cette courbe est une version lissée de la fonction "marche d'escalier":
Si $\sigma$ avait été une fonction en marche d'escalier, alors le neurone sigmoïde aurait été un perceptron, puisque la sortie aurait été soit $0$ soit $1$ selon le signe de $w\cdot x+b$* * En réalité, lorsque $w \cdot x +b = 0$, le perceptron produit en sortie un $0$, tandis que la fonction "marche d'escalier" produit un $1$. Ainsi, pour être rigoureux, nous devrions modifier la fonction "marche d'escalier" en ce point. Mais vous voyez l'idée générale.. En utilisant la vraie fonction $\sigma$ nous obtenons, comme déjà mentionné précédemment, un perceptron lissé. En effet, c'est la régularité de la fonction $\sigma$ qui est le point crucial, et non les détails de sa forme. La régularité de $\sigma$ signifie qu'une petite modification $\Delta w_j$ dans les poids et $\Delta b$ dans le biais va provoquer une petite modification $\Delta \mbox{sortie}$ sur la sortie du neurone. En fait, le calcul différentiel nous dit que l'on obtient une bonne approximation de $\Delta \mbox{sortie}$ avec \begin{eqnarray} \Delta \mbox{sortie} \approx \sum_j \frac{\partial \, \mbox{sortie}}{\partial w_j} \Delta w_j + \frac{\partial \, \mbox{sortie}}{\partial b} \Delta b, \tag{5}\end{eqnarray} où la somme porte sur tous les poids $w_j$, et $\partial \, \mbox{sortie} / \partial w_j$ et $\partial \, \mbox{sortie} /\partial b$ désignent les dérivées partielles de la $\mbox{sortie}$ par rapport à $w_j$ et à $b$, respectivement. Ne vous inquiétez pas si vous n'êtes pas à l'aise avec les dérivées partielles! Même si l'expression ci-dessus semble compliquée avec toutes ces dérivées partielles, elle dit en fait quelque chose de très simple (et c'est une bonne nouvelle): $\Delta\mbox{sortie}$ est une combinaison linéaire des accroissements $\Delta w_j$ et $\Delta b$ des poids et du biais. Cette linéarité facilite le choix des petites modifications à faire subir aux poids et au biais pour obtenir la petite modification souhaitée de la sortie. Ainsi, en plus de posséder les mêmes propriétés qualitatives que les perceptrons, les neurones sigmoïdes rendent beaucoup plus compréhensible la façon dont les changements sur les poids et les biais vont modifier la sortie.
Si c'est la forme de la courbe de $\sigma$ qui importe réellement, et pas sa formule exacte, alors pourquoi utiliser la formule particulière (3)? En fait, plus loin dans le livre, nous considérerons parfois des neurones dont la sortie est $f(w \cdot x + b)$ avec une autre fonction d'activation $f(\cdot)$. Le principal changement lorsque nous utilisons une autre fonction d'activation est que les valeurs particulières des dérivées partielles dans l'équation (5) vont changer. Il se trouve que lorsque nous calculerons ces dérivées partielles plus tard, le fait d'utiliser la fonction $\sigma$ simplifiera les calculs, simplement du fait des propriétés agréables de la fonction exponentielle vis-à-vis de la dérivation. Quoi qu'il en soit, $\sigma$ est souvent utilisée dans les travaux sur les réseaux de neurones, et sera la fonction d'activation que nous utiliserons le plus souvent dans ce livre.
Comment devons-nous interpréter la sortie d'un neurone sigmoïde? Une différence évidente entre les perceptrons et les neurones sigmoïdes est que les neurones sigmoïdes ne produisent pas seulement $0$ ou $1$ en sortie. Leur sortie peut être n'importe quel nombre réel compris entre $0$ and $1$, de sorte que des valeurs telles que $0.173\ldots$ et $0.689\ldots$ sont des sorties possibles. Cela peut être utile, si par exemple nous souhaitons utiliser la valeur de sortie pour représenter l'intensité moyenne des pixels d'une image donnée en entrée d'un réseau neuronal. Mais dans certains cas, cela peut être embêtant. Imaginons que nous souhaitions que la sortie du réseau indique si "l'image d'entrée est un 9" ou si "l'image d'entrée n'est pas un 9". Evidemment, il serait plus simple de réaliser cela si la sortie était soit un $0$ soit un $1$ comme avec un perceptron. Mais en pratique, nous pouvons établir une convention pour régler ce problème, par exemple en décidant d'interpréter toute sortie au-dessus de $0,5$ comme indiquant un "9", et toute sortie en-dessous de $0,5$ comme indiquant l'absence de "9". Lorsque j'utiliserai cette convention, je l'indiquerai toujours explicitement pour qu'il n'y ait pas de confusion.
Exercices
- Des neurones sigmoïdes qui simulent des perceptrons, partie I $\mbox{}$
Supposons que nous prenions tous les poids et les biais dans un réseau de perceptrons, et que nous les multipliions par une constante strictement positive, $c > 0$. Démontrer que le comportement du réseau n'est pas modifié. - Des neurones sigmoïdes qui simulent des perceptrons, partie II $\mbox{}$
Supposons que nous ayons la même situation que dans le problème précédent - un réseau de perceptrons. Supposons aussi que l'on ait choisi l'entrée globale du réseau de perceptrons. Nous n'avons pas besoin de connaître la valeur des entrées, nous avons seulement besoin de savoir que les entrées sont fixées. Sussposons que les poids et les biais soient tels que $w \cdot x + b \neq 0$ pour l'entrée $x$ de n'importe quel perceptron particulier du réseau. Maintenant, remplaçons tous les perceptrons du réseau par des neurones sigmoïdes, et multiplions tous les poids et les biais par une constante strictement positive $c > 0$. Démontrer que lorsque $c$ tend vers $+\infty$ le comportement de ce réseau de neurones sigmoïdes est exactement le même que celui du réseau de perceptrons. Comment ceci peut-il être mis en défaut lorsque $w \cdot x + b = 0$ pour l'un des perceptrons?
L'architecture des réseaux neuronaux
Dans la prochaine section, je vais présenter un réseau neuronal capable de bien reconnaître les chiffres manuscrits. En guise de préparation, il est bon d'expliquer quelques termes qui nous permettront de nommer les différentes parties du réseau. Supposons que nous ayons le réseau :
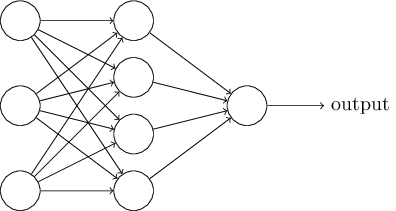

La conception des couches d'entrée et de sortie d'un réseau est souvent simple et directe. Supposons par exemple que nous essayions de déterminer si une image représente un "9" ou non. Une façon naturelle de concevoir le réseau est d'encoder les intensités des pixels de l'image dans les neurones d'entrée. Si l'image est en noir et blanc et que sa taille est $64\times 64$ , alors nous aurons $4096 = 64 \times 64$ neurones d'entrée, avec des intensités convenablement choisies entre $0$ et $1$ pour représenter les niveaux de gris. La couche de sortie contiendra un seul neurone, qui indiquera que "l'image n'est pas un 9" si sa sortie est inférieure à $0,5$ et que "l'image est un 9" si sa sortie est supérieure à $0,5$.
Alors que la conception des couches d'entrée et de sortie d'un réseau neuronal est souvent simple à effectuer, c'est parfois tout un art de concevoir les couches cachées. Il n'est pas possible de résumer le processus de conception des couches cachées par quelques règles générales simples. Au lieu de cela, les chercheurs en réseaux de neurones ont développé de nombreuses règles heuristiques pour la conception des couches cachées, qui permettent d'aider à obtenir le comportement souhaité pour le réseau. Par exemple, de telles règles heuristiques peuvent servir à déterminer comment trouver le bon équilibre entre le nombre de couches cachées et le temps de calcul nécessaire pour entrainer le réseau. Nous rencontrerons plusieurs de ces règles heuristiques de conception plus loin dans le livre.
Jusqu'à maintenant, nous avons parlé des réseaux de neurones dans lesquels la sortie d'une couche est utilisée comme entrée de la couche suivante. De tels réseaux sont appelés réseaux de neurones à propagation avant (feedforward networks). Cela signifie qu'il n'y a pas de boucles dans le réseau - l'information circule toujours vers l'avant, jamais vers l'arrière. Si nous avions des boucles, nous arriverions à une situation dans laquelle les entrées de la fonction $\sigma$ dépendraient de la sortie. Les choses seraient difficiles à appréhender, donc nous n'accepterons pas de telles boucles par la suite.
Il existe cependant d'autres modèles de réseaux de neurones artificiels dans lesquels des boucles de rétroaction sont possibles. Ces modèles sont appelés réseaux de neurones récurrents. L'idée derrière ces modèles est d'utiliser des neurones qui s'activent pendant une durée limitée, avant de s'éteindre. Cette activation peut stimuler d'autres neurones, qui peuvent s'activer un petit peu plus tard, eux aussi pendant une durée limitée. Ceci conduit encore d'autres neurones à s'activer, et nous obtenons une réaction en chaîne d'activations de neurones. Dans ce modèle, les boucles ne posent pas de problèmes parce que la sortie d'un neurone n'affecte son entrée que plus tard, et non instantanément.
Les réseaux de neurones récurrents ont eu moins d'influence que les réseaux à propagation avant, en partie parce que les algorithmes d'apprentissage pour les réseaux récurrents sont (aujourd'hui en tout cas) moins puissants. Mais les réseaux récurrents restent malgré cela extrêmement intéressants. Ils sont plus proches de la façon dont nos cerveaux humains fonctionnent que ne le sont les réseaux à propagation avant. Et il se pourrait que les réseaux récurrents soient capables de résoudre des problèmes qu'un réseau à propagation avant aurait beaucoup de mal à résoudre. Cependant, pour ne pas aller trop loin, nous allons nous concentrer dans ce livre sur les réseaux à propagation avant, qui sont les plus communément utilisés.
Un réseau simple pour reconnaître les chiffres manuscrits
Maintenant que nous avons défini les réseaux de neurones, revenons au problème de la reconnaissance de chiffres manuscrits. Nous pouvons diviser ce problème en deux sous-problèmes. Premièrement, nous souhaiterions avoir un moyen de découper une image qui contient beaucoup de chiffres en une suite d'images séparées contenant chacune un seul chiffre. Par exemple, nous souhaiterions découper l'image
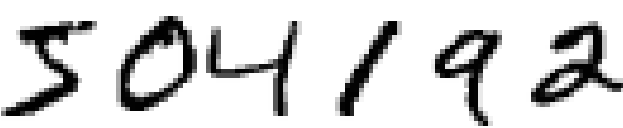
en six images séparées,

Nous humains résolvons facilement ce problème de segmentation, mais pour un ordinateur, il est difficile de découper correctement l'image. Une fois que l'image a été segmentée, le programme doit classifier chaque chiffre isolé. Ainsi, nous souhaiterions par exemple que notre programme reconnaisse que le premier chiffre ci-dessus,
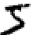
est un 5.
Nous allons nous concentrer sur l'écriture d'un programme qui résout le second problème, à savoir la classification des chiffres individuels. Nous faisons cela car il s'avère que le problème de la segmentation n'est pas si difficile à résoudre, une fois que vous êtes capable de classifier correctement des chiffres individuels. Il existe de nombreuses approches pour résoudre le problème de la segmentation. L'une des approches consiste à tester différentes façons de segmenter l'image, en utilisant un classifieur de chiffres individuels pour évaluer chaque tentative de segmentation. Une tentative de segmentation obtient un score élevé si le classifieur de chiffres individuels a confiance dans la classification de tous les morceaux d'image, et un faible score s'il rencontre des difficultés sur un ou plusieurs des morceaux. L'idée est que si le classifieur rencontre des difficultés, c'est probablement parce que la segmentation choisie est incorrecte. Cette idée et d'autres variantes peuvent être utilisées pour résoudre le problème de la segmentation de façon tout à fait satisfaisante. Ainsi, plutôt que de nous préoccuper de la segmentation, nous allons nous concentrer sur le développement d'un réseau de neurones capable de résoudre le problème à la fois le plus difficile et le plus intéressant, à savoir la reconnaissance de chiffres manuscrits isolés.
Afin de reconnaître des chiffres isolés, nous allons utiliser un réseau neuronal à trois couches:
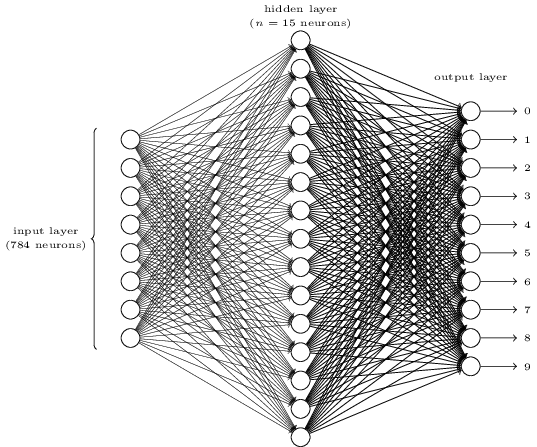
La couche d'entrée du réseau encode les valeurs des pixels d'entrée. Comme nous le verrons dans la prochaine section, nos données d'entrainement pour le réseau seront constituées de nombreuses images de chiffres manuscrits scannés de $28$ pixels sur $28$ pixels, ce qui fait que la couche d'entrée contiendra $784 = 28\times 28$ neurones. Pour simplifier, j'ai omis la plus grande partie des $784$ neurones d'entrée dans le diagramme ci-dessus. Les neurones d'entrée représentent un niveau de gris, la valeur $0.0$ représentant le blanc, la valeur $1.0$ noir, et les valeurs intermédiaires des nuances de gris de plus en plus sombres.
La deuxième couche du réseau est une couche cachée. Nous noterons $n$ le nombre de neurones de cette couche cachée, et nous expérimenterons différentes valeurs pour $n$. L'exemple représenté montre une petite couche cachée, contenant seulement $n = 15$ neurones.
La couche de sortie du réseau contient 10 neurones. Si le premier neurone s'active, c'est-à-dire si sa sortie est $\approx 1$, alors cela indiquera que le réseau pense que le chiffre est un $0$. Si le deuxième neurone s'active, alors cela indiquera que le réseau pense que le chiffre est un $1$, et ainsi de suite. De façon plus précise, nous numérotons les neurones de sortie de $0$ à $9$, et nous regarderons quel est le neurone qui a la plus grande valeur d'activation. S'il s'agit, disons, du neurone numéro $6$, alors notre réseau pense que le chiffre donné en entrée était un $6$. Et ainsi de suite pour les autres neurones de sortie.
Vous vous demandez peut-être pourquoi nous utilisons $10$ neurones de sortie. Après tout, l'objectif du réseau est de nous dire quel chiffre ($0, 1, 2, \ldots, 9$) correspond à l'image d'entrée. Une manière qui pourrait sembler naturelle de faire cela serait d'utiliser seulement $4$ neurones de sortie, et de considérer que chaque neurone code une valeur binaire, selon que sa valeur de sortie est plus proche de $0$ ou de $1$. Quatre neurones suffisent pour encoder la réponse, puisque $2^4 = 16$ dépasse les 10 valeurs possibles pour le chiffre d'entrée. Alors pourquoi notre réseau devrait-il utiliser $10$ neurones? N'est-ce pas inefficace? Je vais donner une justification empirique: nous pouvons essayer les deux façons de concevoir le réseau et il s'avère que, pour ce problème particulier, le réseau avec $10$ neurones en sortie apprend mieux à reconnaître les chiffres que le réseau avec $4$ neurones en sortie. Mais ceci ne répond à la question: Pourquoi le fait d'utiliser $10$ neurones fonctionne mieux? Existe-t-il une méthode heuristique qui nous dirait à l'avance que nous devrions utiliser le codage à $10$ sorties plutôt que le codage à $4$ sorties?
Pour comprendre pourquoi nous faisons cela, il est utile de revenir aux principes fondateurs des réseaux de neurones. Considérons d'abord la situation où nous utilisons $10$ neurones de sortie. Concentrons-nous sur le premier neurone de sortie, celui qui essaie de décider si oui ou non le chiffre est un $0$. Il effectue ceci en soupesant les données issues de la couche cachée de neurones. Que font ces neurones cachés? Eh bien, supposons (juste pour l'explication) que le premier neurone de la couche cachée détecte si une image telle que la suivante est présente ou pas:

Il peut faire cela en attribuant un poids plus important aux pixels d'entrée qui se superposent à cette image, et un poids faible aux autres entrées. De même, supposons (juste pour l'explication) que le deuxième, le troisième et le quatrième neurone de la couche cachée détectent si les images suivantes sont présentes ou pas:

Comme vous l'avez sans doute deviné, ces images forment à elles quatre l'image du $0$ que nous avons vue dans la ligne de chiffres vue précédemment:

Ainsi, si chacun de ces quatre neurones cachés sont activés, nous pouvons conclure que le chiffre est un $0$. Bien sûr, ce n'est pas la seule disposition de pixels qui nous amènera à conclure que l'image est un $0$ - nous pourrions légitimement obtenir un $0$ de différentes façons (disons, par des translations des images ci-dessus ou de légères distorsions). Mais il semble assuré qu'au moins dans ce cas, nous pourrions conclure que l'entrée était un $0$.
En supposant que le réseau de neurones fonctionne de cette façon, nous pouvons donner une explication plausible au fait qu'il est préférable que le réseau possède $10$ sorties plutôt que $4$. Si nous avions $4$ sorties, alors le premier neurone chercherait à décider quel est le bit de poids fort du chiffre en entrée écrit en binaire. Et il n'existe pas de moyen simple de relier ce bit de poids fort à des formes basiques telles que celles vues ci-dessus. Il est difficile d'imaginer qu'il y ait de bonnes raisons historiques pour que les formes qui composent le chiffre dessiné soient liées (disons) au bit de poids fort de la sortie.
Maintenant, ceci étant dit, il s'agit juste d'une méthode heuristique. Rien ne dit que le réseau de neurones à trois couches doive opérer de la façon que j'ai décrite, dans laquelle les neurones cachés détectent des morceaux de formes simples. Peut-être qu'un algorithme d'apprentissage intelligent trouvera une répartition des poids qui permet de n'utiliser que $4$ neurones de sortie. Mais en tant que méthode heuristique, la façon de penser que j'ai décrite fonctionne très bien, et vous économisera beaucoup de temps dans la conception de bonnes architectures de réseaux neuronaux.
Exercice
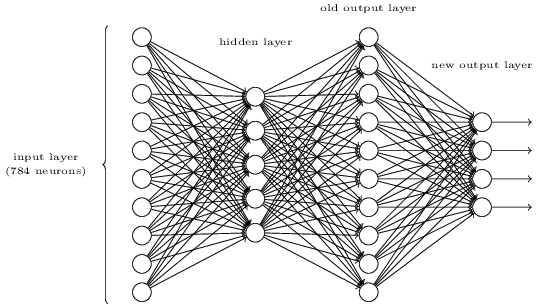
- Il existe une façon de déterminer la représentation bit par bit d'un chiffre en ajoutant une couche supplémentaire au réseau à trois couches ci-dessus. La couche supplémentaire convertit la sortie de la couche précédente en une représentation binaire, comme le montre la figure ci-dessous. Trouvez un ensemble de poids et de biais pour la nouvelle couche de sortie. Supposez que les $3$ premières couches de neurones sont telles que la sortie correcte de la troisième couche (l'ancienne couche de sortie) ait une activation supérieure à $0,99$, et que les sorties incorrectes aient une activation inférieure à $0,01$.
Apprendre avec la descente de gradient
Maintenant que nous avons conçu l'architecture de notre réseau de neurones, comment peut-il apprendre à reconnaître des chiffres? La première chose dont nous aurons besoin est une base de données à partir de laquelle apprendre - ce qu'on appelle les données d'entrainement. Nous utiliserons la base de données MNIST, qui contient des dizaines de milliers d'images scannées de chiffres manuscrits, ainsi que leur classification correcte. Le nom MNIST provient du fait qu'il s'agit d'un sous-ensemble modifié issu de deux ensembles de données rassemblées par NIST, l'Institut National Américain des Standards et de la Technologie. Voici quelques images issues de MNIST:

Comme vous pouvez le voir, ces chiffres sont en fait les mêmes que ceux présentés au début de ce chapitre comme défi aux lecteurs. Bien sûr, lorsque nous testerons notre réseau, nous lui demanderons de reconnaître des images qui ne font pas partie des données d'entrainement!
Les données du MNIST sont formées de deux parties. La première partie contient 60 000 images destinées à être utilisées comme données d'entrainement. Ces images ont été scannées à partir d'échantillons manuscrits provenant de 250 personnes, dont la moitié étaient des employés du Bureau de Recensement américain, l'autre moitié étant formée d'étudiants. Les images sont en noir et blanc (niveaux de gris) avec une taille de 28x28 pixels. La seconde partie de la base de données MNIST est constituée de 10 000 images destinées à être utilisées comme des données de test. Elles sont également de taille 28x28 et en niveaux de gris. Nous utiliserons les données de test pour évaluer si notre réseau de neurones a bien appris à reconnaître les chiffres. Afin d'obtenir un bon test de performance, les données de test sont issues d'un ensemble de 250 personnes différentes de celles des données d'entrainement (avec encore à la fois des employés du Bureau de Recensement et des étudiants). Ceci nous permettra d'être plus confiants dans la capacité de notre système à reconnaître des chiffres écrits par des personnes dont il n'aura pas vu l'écriture pendant la phase d'entrainement.
Nous noterons $x$ les entrées d'entrainement. Il sera plus pratique de considérer chaque entrée d'entrainement $x$ comme un vecteur à $28 \times 28 = 784$ dimensions. Chaque composante du vecteur représente le niveau de gris d'un pixel de l'image. Nous noterons $y = y(x)$ la sortie correspondante souhaitée, où $y$ est un vecteur à $10$ dimensions. Par exemple, si une image d'entrainement particulière, $x$, représente un $6$, alors la sortie souhaitée du réseau est $y(x) = (0, 0, 0, 0, 0, 0, 1, 0, 0, 0)^T$. Notez que $T$ est ici l'opération de transposition, qui transforme un vecteur-ligne en un vecteur (colonne) ordinaire.
Ce que nous aimerions, c'est un algorithme qui nous permette de déterminer les poids et les biais de telle sorte que les sorties du réseau donnent approximativement $y(x)$ pour toutes les entrées d'entrainement $x$. Pour quantifier à quel point notre objectif est réalisé, nous définissons une fonction de coût* *Parfois appelée une fonction de perte ou une fonction objectif. Nous utilisons le terme fonction de coût dans ce livre, mais vous devez connaître les autres dénominations car elles sont souvent utilisées dans les articles de recherche et dans les discussions sur les réseaux neuronaux. : \begin{eqnarray} C(w,b) \equiv \frac{1}{2n} \sum_x \| y(x) - a\|^2. \tag{6}\end{eqnarray} Ici, $w$ désigne l'ensemble de tous les poids du réseau, $b$ tous les poids, $n$ est le nombre total d'entrées d'entrainement, $a$ est le vecteur des sorties du réseau lorsqu'il reçoit $x$ en entrée, et la somme porte sur toutes les entrées d'entrainement, $x$. Bien sûr, la sortie $a$ dépend de $x$, $w$ et $b$, mais afin que les notations restent simples, je n'ai pas fait apparaître explicitement cette dépendance. La notation $\| v \|$ désigne la longueur ou la norme d'un vecteur $v$. Nous appellerons $C$ la fonction de coût quadratique; on l'appelle aussi parfois l'erreur quadratique moyenne ou EQM. En examinant la formule de la fonction coût quadratique, nous voyons que $C(w,b)$ est positif, puisque chacun des termes de la somme est positif. De plus, le coût $C(w,b)$ devient petit, c'est-à-dire $C(w,b) \approx 0$, précisément lorsque $y(x)$ est approximativement égal à la sortie, $a$, pour toutes les entrées d'entrainement, $x$. Ainsi, notre algorithme d'entrainement a fait un bon travail s'il est capable de trouver des poids et des biais tels que $C(w,b) \approx 0$. Au contraire, il n'a pas si bien travaillé lorsque $C(w,b)$ est grand - cela signifierait que $y(x)$ n'est pas si proche de la sortie $a$ pour un grand nombre d'entrées. Ainsi, le but de notre algorithme d'entrainement sera de minimiser le coût $C(w,b)$, vu comme une fonction des poids et des biais. En d'autres termes, nous voulons trouver un ensemble de poids et de biais qui rende le coût aussi faible que possible. Nous ferons cela en utilisant un algorithme connu sous de nom de descente de gradient.
Pourquoi introduire le coût quadratique? Après tout, est-ce que ce n'est pas le nombre d'images correctement classifiées par le réseau qui nous intéresse en premier lieu? Pourquoi ne pas essayer de maximiser ce nombre directement, plutôt que de minimiser une quantité intermédiaire telle que le coût quadratique? Le problème est que le nombre d'images correctement classifiées n'est pas une fonction régulière ou continue des poids et des biais du réseau. Le plus souvent, des petits changements dans les poids et les biais ne provoqueront aucun changement dans le nombre d'images correctement classifiées. Ceci rend la modification des poids et des biais pour obtenir de meilleures performances difficile à déterminer. Si au lieu de cela, nous utilisons une fonction de coût régulière comme le coût quadratique, il devient facile de déterminer les petites modifications à faire subir aux poids et aux biais afin d'obtenir une diminution du coût. C'est pourquoi nous allons d'abord nous concentrer sur la minimisation du coût quadratique, et c'est seulement dans un second temps que nous nous intéresserons à la précision de la classification.
Même si nous voulons utiliser une fonction de coût régulière, peut-être que vous vous demandez encore pourquoi nous choisissons la fonction quadratique comme dans l'équation (6) . Ne serait-ce pas plutôt un choix adapté uniquement à cette situation? Peut-être que si nous avions choisi une fonction de coût différente, nous aurions obtenu un ensemble de poids et de biais complètement différent comme solution optimale. Cette question est légitime et plus tard, nous reviendrons sur le choix de la fonction de coût et nous la modifierons. Cependant, la fonction de coût quadratique de l'équation (6) fonctionne parfaitement bien pour comprendre les bases de l'apprentissage dans les réseaux de neurones, donc nous nous en tiendrons à elle pour le moment.
Pour résumer, notre but lors de la phase d'entrainement d'un réseau de neurones est de déterminer les poids et les biais qui minimisent la fonction de coût quadratique $C(w, b)$. Il s'agit d'un problème bien défini, mais dont la richesse de la structure peut s'avérer gênante - l'interprétation de $w$ et $b$ en tant que poids et biais, la fonction $\sigma$ cachée en arrière-plan, le choix de l'architecture du réseau, MNIST, etc... Il se trouve que nous pouvons comprendre beaucoup de choses en ignorant la plus grosse partie de cette structure, et en nous concentrant seulement sur l'aspect minimisation. Ainsi, pour l'instant, nous allons tout oublier concernant la forme spécifique de la fonction de coût, le lien avec les réseaux de neurones etc... Au lieu de cela, nous allons imaginer que l'on dispose d'une fonction à plusieurs variables et que nous souhaitons minimiser cette fonction. Nous allons présenter une technique appelée descente de gradient qui peut être utilisée pour résoudre de tels problèmes de minimisation. Ensuite nous reviendrons à la fonction spécifique que nous voulons minimiser pour les réseaux de neurones.
Supposons donc que nous essayions de minimiser une fonction, $C(v)$. Cela pourrait être n'importe quelle fonction à valeurs réelles et à plusieurs variables, $v = v_1, v_2, \ldots$. Remarquez que j'ai remplacé les $w$ et les $b$ par $v$ pour unifier les notations et souligner le fait qu'il peut s'agir de n'importe quelle fonction - nous ne pensons plus spécifiquement au contexte des réseaux de neurones. Pour comprendre comment minimiser $C(v)$, il est plus facile d'imaginer que $C$ est une fontion de deux variables seulement, que nous appellerons $v_1$ et $v_2$:
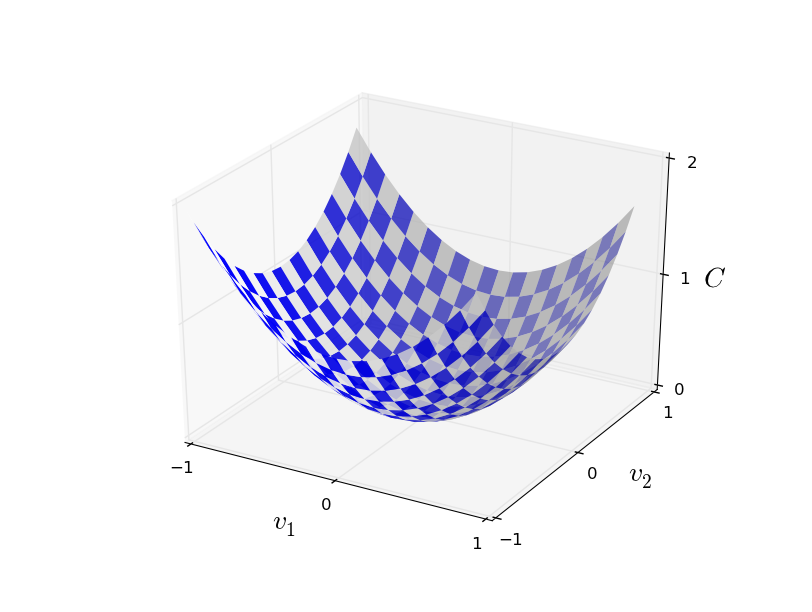
Notre objectif est de trouver où $C$ atteint son minimum global. Bien sûr, pour la fonction représentée ci-dessus, nous pouvons examiner le graphique et trouver le minimum. Dans un sens, la fonction que j'ai choisi de représenter est peut-être légèrement trop simple! Une fonction quelconque, $C$, pourrait être une fonction compliquée, avec beaucoup de variables, et il ne serait alors généralement pas possible de se contenter de regarder le graphique pour trouver le minimum.
Une façon de s'attaquer au problème est d'utiliser le calcul différentiel pour essayer de trouver le minimum analytiquement. Nous pourrions calculer des dérivées puis essayer de les utiliser pour déterminer à quels endroits $C$ possède un extremum. Avec un peu de chance, ceci pourrait fonctionner lorsque $C$ est une fonction de seulement quelques variables. Mais cela tournerait au cauchemar lorsque nous avons beaucoup plus de variables. Et pour les réseaux de neurones, nous aurons souvent beaucoup plus de variables - les plus gros réseaux de neurones ont des fonctions de coût qui dépendent de milliards de poids et de biais, et ce d'une façon extrêmement compliquée. Utiliser le calcul différentiel pour trouver le minimum ne fonctionnera tout simplement pas dans ce cas!
(Après avoir affirmé que nous gagnerions en compréhension en imaginant $C$ comme étant une fonction de seulement deux variables, j'ai tourné en rond pendant deux paragraphes pour dire : "hé, mais comment fait-on avec une fonction qui a beaucoup plus que deux variables?" J'en suis désolé. Faites-moi confiance quand je dis que cela aide vraiment d'imaginer $C$ comme une fonction de deux variables. Il arrive juste que parfois, cette image vole en éclat, et les deux derniers paragraphes évoquaient ce genre de cas. En mathématiques, une manière fructueuse de penser est de jongler avec de multiples images intuitives, d'apprendre dans quels cas une image est appropriée et dans quels cas elle ne l'est pas.)
Nous disions donc que le calcul différentiel ne fonctionne pas. Heureusement, il existe une belle analogie qui suggère un algorithme qui fonctionne très bien. Commençons par imaginer notre fonction comme une sorte de vallée. Si vous plissez un peu les yeux en regardant le graphique plus haut, cela ne devrait pas être trop difficile. Puis nous imaginons une balle qui roule en suivant la pente de la vallée. Notre expérience du monde physique habituel nous dit que la balle va finir par rouler jusqu'au fond de la vallée. Peut-être que nous pouvons utiliser cette idée pour déterminer un minimum pour la fonction? Nous choisirions un point de départ aléatoire pour une balle (imaginaire), puis nous simulerions le mouvement de la balle au fur et à mesure qu'elle roule vers le fond de la vallée. Nous pourrions effectuer cette simulation simplement en calculant des dérivées (et peut-être des dérivées secondes) de $C$ - ces dérivées nous diraient tout ce que nous avons besoin de savoir sur la "forme" locale de la vallée, et donc comment notre balle devrait rouler.
Ce que je viens d'écrire pourrait vous conduire à penser que je vais maintenant essayer d'écrire les équations du mouvement de Newton pour la balle, en considérant les effets du frottement et de la gravité, etc... En fait, nous n'allons pas prendre au pied de la lettre l'analogie de la balle qui roule - nous sommes en train de chercher un algorithme pour minimiser $C$, et pas en train de développer une simulation précise des lois de la physique! Le point de vue de la balle est là pour stimuler notre imagination, et pas pour restreindre notre pensée. Donc plutôt que de nous perdre dans les détails de la physique, demandons-nous simplement : si nous étions Dieu pour une journée, et que nous pouvions créer nos propres lois de la physique, qui dicteraient à la balle comment elle doit rouler, quelles lois du mouvement devrions-nous choisir afin de faire en sorte que la balle roule toujours jusqu'au fond de la vallée?
Pour préciser la question, pensons à ce qu'il se passe lorsque nous faisons faire à la balle un petit déplacement $\Delta v_1$ dans la direction $v_1$, et un petit déplacement $\Delta v_2$ dans la direction $v_2$. Le calcul différentiel nous dit que $C$ est modifié de la façon suivante: \begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2. \tag{7}\end{eqnarray} Nous allons trouver un moyen de choisir $\Delta v_1$ et $\Delta v_2$ de sorte que $\Delta C$ soit strictement négatif; c'est-à-dire que nous allons les choisir de sorte que la balle roule en descendant dans la vallée. Pour comprendre comment effectuer un tel choix, il sera utile de définir $\Delta v$ comme étant le vecteur des changements de $v$, $\Delta v \equiv (\Delta v_1, \Delta v_2)^T$, où $T$ désigne de nouveau l'opération de transposition, qui transforme les vecteurs lignes en vecteurs colonnes. Nous allons aussi définir le gradient de $C$ comme étant le vecteur des dérivées partielles, $\left(\frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2}\right)^T$. Nous notons le vecteur gradient $\nabla C$, c'est-à-dire: \begin{eqnarray} \nabla C \equiv \left( \frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2} \right)^T. \tag{8}\end{eqnarray} Très bientôt, nous réécrirons la variation $\Delta C$ en fonction de $\Delta v$ et du gradient, $\nabla C$. Avant d'en arriver là, je voudrais toutefois clarifier une chose à propos du gradient, sur laquelle les gens butent parfois. Quand ils rencontrent la notation $\nabla C$ pour la première fois, les gens se demandent parfois comment ils doivent comprendre le symbole $\nabla$. Que signifie exactement $\nabla$ ? En fait, c'est très bien de considérer $\nabla C$ comme un unique objet mathématique - le vecteur défini ci-dessus - qui se trouve être écrit avec deux symboles. De ce point de vue, $\nabla$ est juste un petit bout de notation qui nous indique: "hé, $\nabla C$ est un vecteur gradient". Il existe des points de vue plus avancés où $\nabla$ peut être considéré comme une entité mathématique indépendante à part entière (par exemple comme un opérateur différentiel), mais nous n'aurons pas besoin de tels points de vue.
Avec ces définitions, l'expression (7) pour $\Delta C$ peut se réécrire \begin{eqnarray} \Delta C \approx \nabla C \cdot \Delta v. \tag{9}\end{eqnarray} Cette équation nous aide à comprendre pourquoi $\nabla C$ est appelé le vecteur gradient: $\nabla C$ relie la variation de $v$ à la variation de $C$, exactement comme ce qu'un gradient est censé faire. Mais ce qui est vraiment intéressant avec cette équation, c'est qu'elle nous permet de voir comment choisir $\Delta v$ afin de rendre $\Delta C$ négatif. En particulier, supposons que l'on choisisse \begin{eqnarray} \Delta v = -\eta \nabla C, \tag{10}\end{eqnarray} où $\eta$ est un petit paramètre strictement positif (appelé la vitesse d'apprentissage). Alors l'équation (9) nous dit que $\Delta C \approx -\eta \nabla C \cdot \nabla C = -\eta \|\nabla C\|^2$. Comme $\| \nabla C \|^2 \geq 0$, ceci garantit que $\Delta C \leq 0$, c'est-à-dire que, $C$ va toujours diminuer et jamais augmenter, si nous modifions $v$ selon la règle (10) (dans les limites bien sûr de l'approximation faite dans l'équation (9) ). Ceci est exactement la propriété que nous voulions! Et ainsi nous prendrons l'équation (10) pour définir la "loi du mouvement" de la balle dans notre algorithme de descente de gradient. Autrement dit, nous allons utiliser l'équation (10) pour calculer une valeur pour $\Delta v$, puis faire évoluer la position $v$ de la balle de cette valeur : \begin{eqnarray} v \rightarrow v' = v -\eta \nabla C. \tag{11}\end{eqnarray} Ensuite, nous allons de nouveau utiliser cette règle d'évolution pour effectuer un autre déplacement. Si nous continuons ainsi, encore et encore, nous ferons diminuer $C$ jusqu'à ce que - nous l'espérons - nous atteignions un minimum global.
Pour résumer, l'algorithme de descente de gradient consiste à calculer le gradient $\nabla C$, puis à se déplacer dans la direction opposée, en "descendant" la pente de la vallée, et ce de manière répétitive. Nous pouvons visualiser les choses comme ceci:
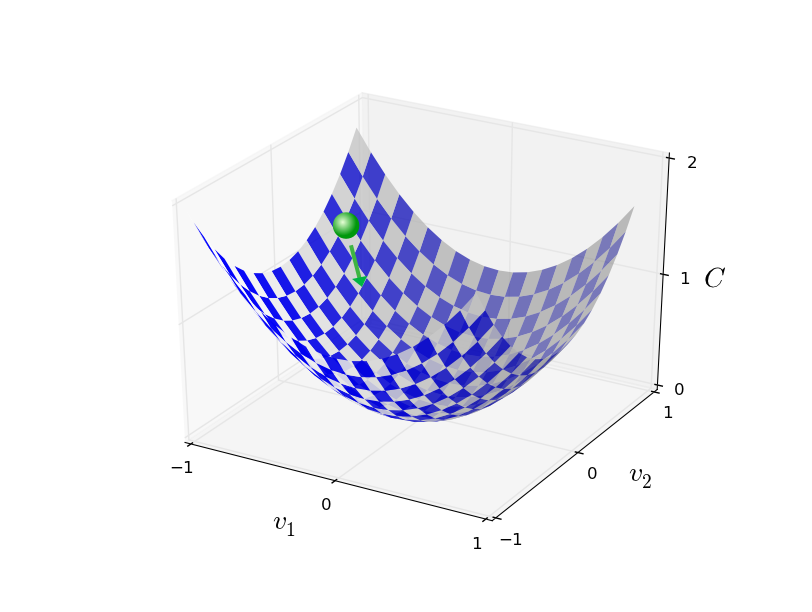
Remarquez qu'avec cette règle, la descente de gradient ne repoduit pas un mouvement physique réel. Dans la réalité, une balle possède une vitesse ou un élan, et cet élan pourrait lui permettre de rouler en travers de la pente, ou même (momentanément) de rouler vers le haut. Ce n'est que par l'effet des forces de frottement que la balle va rouler jusqu'au fond de la vallée. En revanche, notre règle pour choisir $\Delta v$ dit seulement "descend, tout de suite!". Cela reste une très bonne règle pour trouver le minimum!
Afin que la descente de gradient fonctionne correctement, nous devons choisir la vitesse d'apprentissage $\eta$, suffisamment petite pour que l'équation (9) soit une bonne approximation. Sinon, nous risquerions d'aboutir à $\Delta C > 0$, ce qui assurément ne serait pas bon! D'un autre côté, nous ne voulons pas que $\eta$ soit trop petit, car cela rendrait les variations $\Delta v$ minuscules, et ainsi l'algorithme de descente de gradient fonctionnerait très lentement. En pratique, on fait souvent varier $\eta$ de sorte que l'équation (9) soit toujours une bonne approximation, mais que l'algorithme ne soit pas trop lent. Nous verrons plus tard comment procéder.
J'ai expliqué la descente de gradient dans le cas où $C$ est une fonction de deux variables seulement. Mais en fait, tout fonctionne de la même façon lorsque $C$ est une fonction de beaucoup plus de variables. Supposons par exemple que $C$ soit une fonction de $m$ variables, $v_1,\ldots,v_m$. Alors la variation $\Delta C$ de $C$ provoquée par une petite variation $\Delta v = (\Delta v_1,\ldots, \Delta v_m)^T$ est \begin{eqnarray} \Delta C \approx \nabla C \cdot \Delta v, \tag{12}\end{eqnarray} où le gradient $\nabla C$ est le vecteur \begin{eqnarray} \nabla C \equiv \left(\frac{\partial C}{\partial v_1}, \ldots, \frac{\partial C}{\partial v_m}\right)^T. \tag{13}\end{eqnarray} De la même façon que dans le cas à deux variables, nous pouvons choisir \begin{eqnarray} \Delta v = -\eta \nabla C, \tag{14}\end{eqnarray} et nous avons la garantie que notre expression (approchée) (12) pour $\Delta C$ sera négative. Ceci nous donne un moyen de suivre la pente vers le minimum, même dans le cas où $C$ est une fonction de beaucoup de variables, en appliquant de façon répétée la règle de mise à jour \begin{eqnarray} v \rightarrow v' = v-\eta \nabla C. \tag{15}\end{eqnarray} Vous pouvez considérer cette règle de mise à jour comme une définition de l'algorithme de descente de gradient. Elle nous donne un moyen de faire évoluer pas à pas la position $v$ dans le but de déterminer le minimum de la fonction $C$. La règle ne fonctionne pas toujours - plusieurs problèmes peuvent survenir et empêcher la descente de gradient de trouver le minimum global de $C$, nous reviendrons sur ce point dans les chapitres suivants. Mais en pratique, la descente de gradient fonctionne souvent extrêmement bien, et pour ce qui concerne les réseaux de neurones, nous verrons que c'est une manière efficace de minimiser la fonction de coût, et par conséquent d'aider le réseau à apprendre.
En effet, dans un certain sens, la descente de gradient peut être vue comme la stratégie optimale pour chercher un minimum. Supposons que nous essayions d'effectuer un déplacement $\Delta v$ de façon à diminuer $C$ le plus possible. Ceci équivaut à minimiser $\Delta C \approx \nabla C \cdot \Delta v$. Nous allons contraindre la taille du déplacement de sorte que $\|\Delta v \| = \epsilon$ pour un petit $\epsilon > 0$ fixé. Autrement dit, nous voulons un déplacement qui soit un petit pas de taille fixée, et nous allons chercher à trouver la direction du mouvement qui fait diminuer $c$ le plus possible. On peut prouver que le choix de $\Delta v$ qui minimise $\nabla C \cdot \Delta v$ est $\Delta v = - \eta \nabla C$, où $\eta = \epsilon / \|\nabla C\|$ est déterminé par la contrainte sur la taille $\|\Delta v\| = \epsilon$. Ainsi, on peut voir la descente de gradient comme une façon d'effectuer des petits pas dans la meilleure direction pour faire diminuer immédiatement $C$.
Exercices
- Démontrer l'affirmation du dernier paragraphe. Indication: Si vous n'êtes pas déjà familier avec l' inégalité de Cauchy-Schwarz, il pourrait vous être utile de vous familiariser avec elle.
- J'ai expliqué la descente de gradient lorsque $C$ est une fonction de deux variables, et lorsque c'est une fonction de plus de deux variables. Que se passe-t-il lorsque $C$ est une fonction d'une variable seulement? Pouvez-vous donner une interprétation géométrique de ce que fait la descente de gradient dans le cas à une dimension?
Les gens ont expérimenté de nombreuses variantes de la descente de gradient, notamment des variantes qui collent de plus près au vrai mouvement physique d'une balle. Ces variantes qui imitent une balle ont des avantages, mais ont aussi un inconvénient majeur: il s'avère nécessaire de calculer les dérivées partielles secondes de $C$, et ceci peut coûter très cher en temps de calcul. Pour comprendre pourquoi, supposons que nous voulions calculer toutes les dérivées partielles secondes $\partial^2 C/ \partial v_j \partial v_k$. S'il y avait un million de telles variables $v_j$ alors nous aurions besoin de calculer de l'ordre d'un trillion (c'es-à-dire un million au carré) de dérivées partielles secondes* *En fait, plutôt un demi-trillion puisque $\partial^2 C/ \partial v_j \partial v_k = \partial^2 C/ \partial v_k \partial v_j$. Mais vous voyez l'idée.! Cela va devenir très couteux au niveau des calculs. Ceci étant dit, il existe des astuces pour éviter ce genre de problème, et la recherche d'alternatives à la descente de gradient est un domaine de recherche actif. Mais dans ce livre, nous utiliserons la descente de gradient (et quelques variantes) comme approche principale pour l'apprentissage des réseaux de neurones.
Comment pouvons-nous appliquer la descente de gradient pour apprendre avec un réseau de neurones? L'idée est d'utiliser la descente de gradient pour déterminer les poids $w_k$ et les biais $b_l$ qui minimisent le coût dans l'équation (6) . Pour voir comment cela fonctionne, réécrivons la règle de mise à jour de la descente de gradient, en remplaçant les variables $v_j$ par les poids et les biais. Autrement dit, notre "position" a maintenant pour composantes $w_k$ et $b_l$, et le vecteur gradient $\nabla C$ a les composantes correspondantes $\partial C / \partial w_k$ et $\partial C / \partial b_l$. Si nous écrivons la règle de mise à jour de la descente de gradient en termes de composantes, nous obtenons \begin{eqnarray} w_k & \rightarrow & w_k' = w_k-\eta \frac{\partial C}{\partial w_k} \tag{16}\\ b_l & \rightarrow & b_l' = b_l-\eta \frac{\partial C}{\partial b_l}. \tag{17}\end{eqnarray} En appliquant de manière répétée cette règle de mise à jour, nous pouvons "rouler jusqu'en bas de la colline", et espérer trouver un minimum de la fonction de coût. Autrement dit, il s'agit d'une règle qui peut être utilisée pour l'apprentissage dans les réseaux de neurones.
Il existe plusieurs difficultés dans l'application de la règle de descente de gradient. Nous les examinerons dans les chapitres suivants. Mais pour le moment, je veux juste évoquer un problème. Pour le comprendre, revenons au coût quadratique dans l'équation (6) . Remarquez que cette fonction de coût est de la forme $C = \frac{1}{n} \sum_x C_x$, c'est-à-dire que c'est une moyenne des coûts $C_x \equiv \frac{\|y(x)-a\|^2}{2}$ de chaque exemple d'entrainement pris individuellement. En pratique, pour calculer le gradient $\nabla C$, nous devons calculer les gradients $\nabla C_x$ séparément pour chacun des exemples d'entrainement $x$, puis en faire la moyenne $\nabla C = \frac{1}{n}\sum_x \nabla C_x$. Malheureusement, lorsque le nombre d'exemples d'entrainement est très grand, cela peut prendre beaucoup de temps, et l'apprentissage s'effectue très lentement.
Une idée appelée descente de gradient stochastique peut être mise à profit pour accélérer l'apprentissage. L'idée est d'estimer le gradient $\nabla C$ en calculant $\nabla C_x$ pour un petit échantillon d'exemples d'entrainement choisis au hasard. En calculant la moyenne sur ce petit échantillon, il s'avère que nous pouvons obtenir rapidement une bonne estimation du vrai gradient $\nabla C$, et ceci contribue à accélérer la descente de gradient, et donc l'apprentissage.
Précisons ces idées. Le principe de la descente de gradient stochastique est de choisir au hasard un petit nombre $m$ d'exemples d'entrainement. Nous noterons ces entrées d'entrainement $X_1, X_2, \ldots, X_m$, et nous les appellerons un mini-lot. Pourvu que la taille $m$ de l'échantillon soit assez grande, nous pouvons nous attendre à ce que la valeur moyenne des $\nabla C_{X_j}$ soit proche de la moyenne de tous les $\nabla C_x$, c'est-à-dire \begin{eqnarray} \frac{\sum_{j=1}^m \nabla C_{X_{j}}}{m} \approx \frac{\sum_x \nabla C_x}{n} = \nabla C, \tag{18}\end{eqnarray} où la deuxième somme porte sur l'ensemble complet des données d'entrainement. En retournant l'équation, nous obtenons \begin{eqnarray} \nabla C \approx \frac{1}{m} \sum_{j=1}^m \nabla C_{X_{j}}, \tag{19}\end{eqnarray} ce qui confirme que l'on peut estimer le gradient global en calculant seulement les gradients pour le mini-lot choisi au hasard.
Pour relier ceci de manière explicite à l'apprentissage dans les réseaux de neurones, supposons que $w_k$ et $b_l$ désignent les poids et les biais de notre réseau. Alors la descente de gradient stochastique procède en choisissant au hasard un mini-lot d'exemples d'entrainement, et en s'entrainant avec ces derniers: \begin{eqnarray} w_k & \rightarrow & w_k' = w_k-\frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial w_k} \tag{20}\\ b_l & \rightarrow & b_l' = b_l-\frac{\eta}{m} \sum_j \frac{\partial C_{X_j}}{\partial b_l}, \tag{21}\end{eqnarray} où les sommes portent sur tous les exemples d'entrainement $X_j$ du mini-lot courant. Ensuite, nous choisissons au hasard un autre mini-lot et nous effectuons l'entrainement avec celui-ci. Et ainsi de suite, jusqu'à ce que nous ayons épuisé les données d'entrainement. On dit alors qu'on a réalisé un tour complet d'entrainement. A partir de là, on recommence avec un nouveau tour d'entrainement.
Soit dit en passant, remarquons que les conventions ne sont pas toujours les mêmes en ce qui concerne le calibrage de la fonction de coût et de la mise à jour des mini-lots. Dans l'équation (6) nous avons multiplié le coût global par un facteur $\frac{1}{n}$. Les gens omettent parfois le $\frac{1}{n}$, et calculent la somme des coûts de tous les exemples au lieu de calculer une moyenne. Ceci est particulièrement utile lorsque le nombre total d'exemples d'entrainement n'est pas connu à l'avance. Ceci peut arriver si de nouvelles données d'entrainement sont générées en temps réel par exemple. Et de la même façon, les règles de mise à jour du mini-lot (20) and (21) omettent parfois le facteur $\frac{1}{m}$ devant les sommes. Cela ne change pas grand chose fondamentalement, puisque cela revient à changer l'unité de la vitesse d'apprentissage $\eta$. Mais il faut faire attention à cela si on comparer les travaux de différentes personnes.
Nous pouvons envisager la descente de gradient stochastique comme un sondage politique: il est beaucoup plus facile de prélever un mini-lot que d'appliquer la descente de gradient à la totalité du lot, de la même façon qu'effectuer un sondage est plus facile que de procéder à une élection. Si par exemple nous avons un ensemble d'entrainement de taille $n = 60 000$, comme avec les données MNIST, et si nous choisissons une taille de mini-lot disons $m = 10$, cela signifie que nous gagnons un facteur $6 000$ sur la vitesse d'estimation du gradient! Bien sûr, l'estimation ne sera pas parfaite - il y aura des fluctuations statistiques - mais nous n'avons pas besoin qu'elle soit parfaite: tout ce qui nous importe vraiment est de nous déplacer dans une direction générale qui va nous permettre de faire diminuer $C$, et cela signifie que nous n'avons pas besoin d'un calcul exact du gradient. En pratique, la descente de gradient stochastique est une technique très utilisée et puissante pour l'apprentissage dans les réseaux de neurones, et elle est à la base de la plupart des techniques d'apprentissage que nous développerons dans ce livre.
Exercice
- Une version extrême de la descente de gradient est d'utiliser un mini-lot de taille 1. C'est-à-dire qu'étant donné un exemple d'entrainement $x$, nous mettons à jour nos poids et nos biais selon les règles $w_k \rightarrow w_k' = w_k - \eta \partial C_x / \partial w_k$ et $b_l \rightarrow b_l' = b_l - \eta \partial C_x / \partial b_l$. Ensuite nous choisissons un autre exemple d'entrainement, et nous mettons de nouveau à jour les poids et les biais. Et ainsi de suite. Cette procédure est appelée apprentissage en ligne ou incrémental. Avec l'apprentissage incrémental, un réseau de neurones apprend à partir d'un seul exemple à la fois (comme le font les humains). Donnez un avantage et un inconvénient de l'apprentissage incrémental, par rapport à la descente de gradient stochastique avec des mini-lots de taille 20 par exemple.
Permettez-moi de conclure cette section en discutant d'un point qui pose parfois des problèmes aux personnes qui débutent avec la descente de gradient. Dans les réseaux de neurones, le coût $C$ est bien sûr une fonction de nombreuses variables - tous les poids et les biais - et ainsi, dans un certain sens, cette fonction définit une surface dans un espace de très grande dimension. Certaines personnes restent bloquées en se disant: "Hé, je vais devoir visualiser toutes ces dimensions supplémentaires!". Et elles commencent à s'inquiéter: "Je n'arrive déjà pas à penser en quatre dimensions, et encore moins en cinq dimensions (ou cinq millions de dimensions)". Est-ce qu'il leur manque un don spécial, un don que seuls les "vrais" supermathématiciens possèderaient? Bien sûr, la réponse est non. Même les mathématiciens professionnels n'arrivent pas très bien à visualiser les quatre dimensions, voire pas du tout. L'astuce qu'ils utilisent consiste à développer d'autres manières de représenter ce qui se passe. C'est exactement ce que nous avons fait précédemment: nous avons utilisé une représentation algébrique (plutôt que visuelle) de $\Delta C$ pour comprendre comment il faut se déplacer pour diminuer $C$. Les gens qui se débrouillent bien pour penser en grande dimension ont une bibliothèque mentale qui contient de nombreuses techniques; notre astuce algébrique n'est un exemple parmi d'autres. Ces techniques ne sont peut-être pas aussi simples que celles auxquelles nous sommes habitués pour voir en trois dimensions, mais une fois que vous vous êtes construit un catalogue de ce genre de techniques, vous pouvez réussir à penser en haute dimension. Je ne donnerai pas plus de détails ici, mais si cela vous intéresse, vous aimerez probablement lire cette discussion de quelques techniques utilisées par les mathématiciens professionnels pour penser en grande dimension. Même si certaines de ces techniques sont assez complexes, la plupart d'entre elles sont intuitives et accessibles, et peuvent être maîtrisées par n'importe qui.
Implémenter notre réseau pour classifier des chiffres
Bien, écrivons maintenant un programme qui apprend à reconnaître des chiffres manuscrits, à l'aide de la descente de gradient stochastique et de la base de données d'entrainement MNIST. Nous ferons cela avec un court programme écrit en Python 3, qui ne comporte que 74 lignes de code! La première chose à faire est de se procurer les données MNIST. Si vous êtes un utilisateur de git, vous pouvez obtenir ces données en clonant le dépôt du code pour ce livre
git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git
Si vous n'utilisez pas git vous pouvez télécharger les données et le code ici. (Note du traducteur: les programmes dans leur version originale sont écrits en Python 2.7; ceux de la traduction française ont été convertis en Python 3. Le seul moyen d'obtenir une version en Python 3 est de copier/coller les codes des programmes présentés plus bas).
Au passage, lorsque j'ai décrit les données MNIST un peu plus tôt, j'ai dit qu'elles étaient séparées en 60 000 images d'entrainement et 10 000 images de test. Il s'agit de la description officielle de MNIST. En fait, nous allons séparer les données d'une façon un peu différente. Nous allons laisser les images de test telles quelles, mais nous allons séparer les 60 000 images d'entrainement en deux parties: un groupe de 50 000 images que nous utiliserons pour entrainer notre réseau de neurones, et un groupe de validation séparé, constitué de 10 000 images. Nous n'utiliserons pas le groupe de validation dans ce chapitre, mais nous en verrons l'utilité plus loin dans le livre pour nous aider à régler certains hyper-paramètres du réseau de neurones - des choses telles que la vitesse d'apprentissage, etc..., qui ne sont pas directement fixées par notre algorithme d'apprentissage. Bien que les données de validation ne soient pas spécifiées comme telles dans MNIST, beaucoup de monde les utilise de cette façon, et l'utilisation de données de validation est courante pour les réseaux de neurones. A partir de maintenant, lorsque je fais référence aux "données d'entrainement MNIST", je parle de notre groupe de 50 000 images, et pas de l'ensemble original formé des 60 000 images* *Comme dit précédemment, la base de données MNIST est basée sur deux ensembles de données rassemblées par NIST (National Institute of Standards and Technology, l'institut national des normes et de la technologie aux Etats-Unis). Pour construire MNIST, les données du NIST ont été transformées et traduites dans un format plus lisible par Yann LeCun, Corinna Cortes, et Christopher J. C. Burges. Voir ce lien pour plus de détails. L'ensemble de données MNIST situé sur mon dépôt se trouve sous une forme plus facile à charger et à manipuler en Python. J'ai obtenu cette forme particulière auprès du laboratoire d'apprentissage automatique LISA de l'université de Montréal (lien)..
En plus des données MNIST, nous avons également besoin d'une bibliothèque Python appelée Numpy, qui permet d'effectuer de façon performante les calculs d'algèbre linéaire. Si vous n'avez pas déjà installé Numpy, vous le trouverez ici.
Permettez-moi de vous expliquer les caractéristiques qui sont au coeur du code du réseau de neurones, avant de vous donner le code complet. La pièce centrale est une classe Network (réseau en français), que nous utilisons pour représenter un réseau de neurones. Voici le code qui permet d'initialiser un objet Network:
class Network(object):
def __init__(self, sizes):
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
Dans ce code, la liste sizes (tailles en français) contient le nombre de neurones dans chacune des couches. Ainsi par exemple, si nous voulons créer un objet Network avec 2 neurones dans la première couche, trois neurones dans la deuxième couche, et 1 neurone dans la dernière couche, nous le ferons avec cette ligne de code:
net = Network([2, 3, 1])
Remarquez aussi que les biais et les poids sont stockés en tant que listes de matrices Numpy. Ainsi par exemple, net.weights[1] est une matrice Numpy qui contient les poids qui relient la deuxième couche de neurones à la troisième couche. (il ne s'agit pas de la première et de la deuxième couche car l'indexation des listes en Python commence à 0.) Etant donné que net.weights[1] est un peu long à écrire, notons simplement cette matrice $w$. C'est une matrice telle que $w_{jk}$ représente le poids de la connexion entre le $k^{\rm ième}$ neurone de la deuxième couche et le $j^{\rm ième}$ neurone de la troisième couche. L'ordre des indices $j$ et $k$ peut sembler étrange - ne serait-il pas plus logique d'inverser les indices $j$ et $k$? Le gros avantage de cette écriture en sens inverse est qu'elle implique que le vecteur des activations de la troisième couche s'écrit: \begin{eqnarray} a' = \sigma(w a + b). \tag{22}\end{eqnarray} Cette équation est un peu complexe, donc décomposons-la morceau par morceau. $a$ est le vecteur des activations de la deuxième couche de neurones. Pour obtenir $a'$, nous multiplions $a$ par la matrice des poids $w$, puis nous ajoutons le vecteur des biais $b$. Enfin, nous appliquons la fonction $\sigma$ composante par composante au vecteur $w a +b$. (on appelle ceci vectoriser la fonction $\sigma$.) Il est facile de vérifier que l'équation (22) donne le même résultat que notre règle initiale, l'équation (4) , pour calculer la sortie d'un neurone sigmoïde.
Exercice
- Ecrire l'équation (22) composante par composante, et vérifier qu'elle donne le même résultat que la règle (4) pour calculer la sortie d'un neurone sigmoïde.
Ayant vu tout cela, il est facile d'écrire le code qui calcule la sortie d'une instance de la classe Network. Nous commençons par définir la fonction sigmoïde:
def sigmoid
(z):
return 1.0/(1.0+np.exp(-z))
Nous ajoutons ensuite une méthode feedforward à la classe Network, ce qui renvoie, étant donnée une entrée a pour le réseau, la sortie correspondante* *On suppose que l'entrée a est un ndarray de Numpy de dimensions (n, 1), et pas un vecteur de dimension (n,). Ici, n est le nombre d'entrées du réseau. Si vous essayez d'utiliser un vecteur (n,) comme entrée, vous obtiendrez des résultats bizarres. Même si l'utilisation d'un vecteur (n,) semble être un choix plus naturel, l'utilisation d'un ndarray (n, 1) rend particulièrement simple la modification du code pour propager plusieurs entrées à la fois, et cela est parfois plus pratique. Cette méthode se contente d'appliquer l'équation (22) à chaque couche:
def feedforward(self, a):
"""Return the output of the network if "a" is input."""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)
return a
Bien sûr, ce que nous attendons avant tout de nos objets Network est qu'ils apprennent. Pour cela, nous les dotons d'une méthode SGD qui implémente la descente de gradient stochastique. Voici le code. Il peut sembler mystérieux par endroit, mais je le décomposerai juste après le listing.
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""Train the neural network using mini-batch stochastic
gradient descent. The "training_data" is a list of tuples
"(x, y)" representing the training inputs and the desired
outputs. The other non-optional parameters are
self-explanatory. If "test_data" is provided then the
network will be evaluated against the test data after each
epoch, and partial progress printed out. This is useful for
tracking progress, but slows things down substantially."""
if test_data: n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)
La variable training_data est une liste de tuples (x, y) qui représentent les entrées des exemples d'entrainement ainsi que les sorties souhaitées correspondantes. Les variables epochs et mini_batch_size sont ce à quoi vous pouvez vous attendre - le nombre de tours complets à effectuer pour l'entrainement et la taille des mini-lots à utiliser. eta est la vitesse d'apprentissage, $\eta$. Si l'argument optionnel test_data est fourni, alors le programme va évaluer les performances du réseau après chaque tour complet d'entrainement, et afficher le résultat provisoire. Ceci est utile pour suivre la progression, mais ralentit le programme.
Le programme fonctionne de la façon suivante. A chaque tour, il commence par réordonner aléatoirement l'ensemble des données d'entrainement, puis le découpe en mini-lots avec la taille appropriée. Ceci est une façon simple de tirer au hasard des exemples d'entrainement. Ensuite, pour chaque mini_batch (mini-lot), nous appliquons un pas de descente de gradient. Ceci est réalisé par le code self.update_mini_batch(mini_batch, eta), qui met à jour les poids et les biais du réseau après une seule itération de la descente de gradient, à partir des données d'entrainement contenues dans mini_batch. Voici le code de la méthode update_mini_batch:
def update_mini_batch(self, mini_batch, eta):
"""Update the network's weights and biases by applying
gradient descent using backpropagation to a single mini batch.
The "mini_batch" is a list of tuples "(x, y)", and "eta"
is the learning rate."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
Je ne vais pas montrer le code pour self.backprop tout de suite. Nous étudierons comment fonctionne la rétropropagation dans le chapitre suivant, ainsi que le code pour self.backprop. Pour le moment, admettons simplement qu'il fonctionne comme prévu, en renvoyant le gradient de la fonction de coût associé à l'exemple d'entrainement x.
Regardons maintenant le programme complet, qui contient les commentaires de documentation que j'avais omis précédemment. A l'exception de self.backprop, le programme se comprend facilement - le gros du travail est effectué dans self.SGD et self.update_mini_batch, dont nous avons déjà parlé. La méthode self.backprop utilise quelques fonctions supplémentaires pour l'aider à calculer le gradient, notamment sigmoid_prime, qui calcule la dérivée de la fonction $\sigma$, et self.cost_derivative que je ne détaillerai pas ici. Vous pouvez en comprendre l'essentiel (et peut-être aussi les détails) simplement en jetant un coup d'oeil au code et aux commentaires de documentation. Nous les examinerons en détail dans le prochain chapitre. Remarquez que même si le programme semble long, une grosse partie du code est constituée de commentaires de documentation pour faciliter la compréhension. En réalité, le programme ne contient que 74 lignes de code hors commentaire et hors lignes vides. Vous pouvez retrouver le programme complet sur GitHub ici.
"""
network.py
~~~~~~~~~~
A module to implement the stochastic gradient descent learning
algorithm for a feedforward neural network. Gradients are calculated
using backpropagation. Note that I have focused on making the code
simple, easily readable, and easily modifiable. It is not optimized,
and omits many desirable features.
"""
#### Libraries
# Standard library
import random
# Third-party libraries
import numpy as np
class Network(object):
def __init__(self, sizes):
"""The list ``sizes`` contains the number of neurons in the
respective layers of the network. For example, if the list
was [2, 3, 1] then it would be a three-layer network, with the
first layer containing 2 neurons, the second layer 3 neurons,
and the third layer 1 neuron. The biases and weights for the
network are initialized randomly, using a Gaussian
distribution with mean 0, and variance 1. Note that the first
layer is assumed to be an input layer, and by convention we
won't set any biases for those neurons, since biases are only
ever used in computing the outputs from later layers."""
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
def feedforward(self, a):
"""Return the output of the network if ``a`` is input."""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""Train the neural network using mini-batch stochastic
gradient descent. The ``training_data`` is a list of tuples
``(x, y)`` representing the training inputs and the desired
outputs. The other non-optional parameters are
self-explanatory. If ``test_data`` is provided then the
network will be evaluated against the test data after each
epoch, and partial progress printed out. This is useful for
tracking progress, but slows things down substantially."""
if test_data: n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)
def update_mini_batch(self, mini_batch, eta):
"""Update the network's weights and biases by applying
gradient descent using backpropagation to a single mini batch.
The ``mini_batch`` is a list of tuples ``(x, y)``, and ``eta``
is the learning rate."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
def backprop(self, x, y):
"""Return a tuple ``(nabla_b, nabla_w)`` representing the
gradient for the cost function C_x. ``nabla_b`` and
``nabla_w`` are layer-by-layer lists of numpy arrays, similar
to ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# backward pass
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# Note that the variable l in the loop below is used a little
# differently to the notation in Chapter 2 of the book. Here,
# l = 1 means the last layer of neurons, l = 2 is the
# second-last layer, and so on. It's a renumbering of the
# scheme in the book, used here to take advantage of the fact
# that Python can use negative indices in lists.
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
"""Return the number of test inputs for which the neural
network outputs the correct result. Note that the neural
network's output is assumed to be the index of whichever
neuron in the final layer has the highest activation."""
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
def cost_derivative(self, output_activations, y):
"""Return the vector of partial derivatives \partial C_x /
\partial a for the output activations."""
return (output_activations-y)
#### Miscellaneous functions
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))
Notre programme reconnait-il correctement les chiffres manuscrits? Eh bien commençons par charger les données MNIST. Pour cela, je vais utiliser un petit programme utilitaire, mnist_loader.py, qui sera décrit plus bas. Nous exécutons les commandes suivantes dans la console Python,
>>>
import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
Nous aurions bien sûr pu faire cela dans un programme Python, mais cela sera probablement plus facile de saisir les instructions au fur et à mesure dans la console Python.
Après avoir chargé les données MNIST, nous allons initialiser un objet Network avec $30$ neurones cachés. Nous pouvons faire cela après avoir importé le programme Python vu plus haut, dont le nom est network,
>>> import network
>>> net = network.Network([784, 30, 10])
Enfin, nous allons utiliser la descente de gradient stochastique pour apprendre à partir des données MNIST training_data pendant 30 tours, avec des mini-lots de 10 échantillons et une vitesse d'apprentissage $\eta = 3.0$,
>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
Remarquez que le programme va mettre un peu de temps à s'exécuter - pour une machine ordinaire (de 2015) le programme tournera probablement pendant quelques minutes. Si vous exécutez le code en même temps que vous lisez, je vous suggère de laisser le programme tourner, de continuer à lire et de vérifier de temps en temps le résultat du programme. Si vous êtes pressé, vous pouvez accélérer les choses en réduisant le nombre de tours, en réduisant le nombre de neurones cachés, ou en utilisant seulement une partie des données d'entrainement. Notez qu'un code "professionnel" serait beaucoup plus rapide: le but de ces scripts Python est de vous aider à comprendre comment fonctionnent les réseaux de neurones, et pas de réaliser de hautes performances! Et bien sûr, une fois que nous avons entrainé le réseau, il peut tourner très vite sur n'importe quelle machine. Par exemple, une fois que le réseau a appris une bonne combinaison de poids et de biais, on peut facilement le faire tourner en Javascript au sein d'un navigateur internet, ou en tant qu'application native sur un smartphone. Quoi qu'il en soit, voici une transcription partielle de la sortie obtenue après une séance d'entrainement du réseau de neurones. La transcription permet de voir le nombre d'images de test reconnues correctement par le réseau après chaque tour d'entrainement. Comme vous pouvez le constater, après un seul tour, celui-ci est déjà de 9 129 sur 10 000, et ce nombre continue à croître,
Epoch 0: 9129 / 10000
Epoch 1: 9295 / 10000
Epoch 2: 9348 / 10000
...
Epoch 27: 9528 / 10000
Epoch 28: 9542 / 10000
Epoch 29: 9534 / 10000
En fin de compte, le réseau entraîné nous donne un taux de réussite d'environ $95$ pour cent pour la classification - avec un pic à $95,42$ pour cent au tour 28 ! Ceci est très encourageant pour un premier essai. Je dois cependant vous prévenir que si vous exécutez le code, vos résultats ne seront pas exactement les mêmes que les miens, à cause de l'initialisation aléatoire des poids et des biais. Pour obtenir les résultats de ce chapitre, j'ai pris le meilleur résultat sur trois exécutions.
Répétons l'expérience précédente en fixant le nombre de neurones cachés à $100$. Comme précédemment, l'exécution va prendre un certain temps (sur mon ordinateur, cette expérience prend quelques dizaines de secondes pour chaque tour d'entrainement).
>>> net = network.Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 3.0, test_data=test_data)
Clairement, ceci améliore les résultats pour les porter à $96,59$ pour cent de réussite. Dans ce cas au moins, le fait d'utiliser plus de neurones cachés permet d'obtenir de meilleurs résultats* *Les lecteurs m'ont fait part de résultats très variables pour cette expérience, et certaines exécutions donnent des résultats moins bons que précédemment. L'utilisation des techniques introduites au chapitre 3 permettra de réduire nettement les variations de performances obtenues lors des différentes séances d'entrainement de nos réseaux.
Bien sûr, pour obtenir d'aussi bons résultats, il m'a fallu effectuer des choix spécifiques pour le nombre de tours d'entrainement, la taille des mini-lots et la vitesse d'apprentissage $\eta$. Comme je l'ai dit précédemment, ces nombres sont appelés des hyper-paramètres, afin de les distinguer des paramètres (poids et biais) appris par notre algorithme d'apprentissage. Supposons par exemple que nous ayons choisi une vitesse d'apprentissage $\eta = 0.001$,
>>> net = network.Network([784, 100, 10])
>>> net.SGD(training_data, 30, 10, 0.001, test_data=test_data)
Les résultats sont beaucoup moins prometteurs,
Epoch 0: 1139 / 10000
Epoch 1: 1136 / 10000
Epoch 2: 1135 / 10000
...
Epoch 27: 2101 / 10000
Epoch 28: 2123 / 10000
Epoch 29: 2142 / 10000
En général, il est difficile de débugger un réseau de neurones, particulièrement lorsque le choix initial des hyper-paramètres ne donne pas de meilleurs résultats qu'un bruit aléatoire. Supposons que nous reprenions la bonne architecture de réseau avec 30 neurones cachés, mais avec une vitesse d'apprentissage $\eta = 100.0$:
>>> net = network.Network([784, 30, 10])
>>> net.SGD(training_data, 30, 10, 100.0, test_data=test_data)
Epoch 0: 1009 / 10000
Epoch 1: 1009 / 10000
Epoch 2: 1009 / 10000
Epoch 3: 1009 / 10000
...
Epoch 27: 982 / 10000
Epoch 28: 982 / 10000
Epoch 29: 982 / 10000
La leçon qu'il faut tirer de tout cela est que débugger un réseau de neurone n'est pas simple, et comme pour la programmation ordinaire, c'est tout un art. Vous devez apprendre l'art du débogage si vous voulez obtenir de bons résultats avec vos réseaux de neurones. Plus généralement, nous devons développer des méthodes heuristiques pour choisir de bons hyper-paramètres et une bonne architecture. Nous discuterons longuement de ces thèmes dans la suite du livre, et notamment de la façon dont j'ai choisi les hyper-paramètres dans l'exemple précédent.
Exercice
- Essayez de créer un réseau à seulement deux couches - une couche d'entrée et une couche de sortie, pas de couche cachée - possédant respectivement 784 et 10 neurones. Entrainez le réseau avec la descente de gradient stochastique. Quel taux de réussite obtenez-vous pour la classification?
Auparavant, j'ai omis de préciser comment les données MNIST sont chargées. C'est assez direct. Pour être complet, voici le code. Les structures de données utilisées pour stocker les données MNIST sont décrites dans les commentaires de documentation - c'est assez simple, des tuples et des listes d'objets Numpy ndarray (vous pouvez les considérer comme des vecteurs si vous n'êtes pas familier avec les ndarray):
"""
mnist_loader
~~~~~~~~~~~~
A library to load the MNIST image data. For details of the data
structures that are returned, see the doc strings for ``load_data``
and ``load_data_wrapper``. In practice, ``load_data_wrapper`` is the
function usually called by our neural network code.
"""
#### Libraries
# Standard library
import cPickle
import gzip
# Third-party libraries
import numpy as np
def load_data():
"""Return the MNIST data as a tuple containing the training data,
the validation data, and the test data.
The ``training_data`` is returned as a tuple with two entries.
The first entry contains the actual training images. This is a
numpy ndarray with 50,000 entries. Each entry is, in turn, a
numpy ndarray with 784 values, representing the 28 * 28 = 784
pixels in a single MNIST image.
The second entry in the ``training_data`` tuple is a numpy ndarray
containing 50,000 entries. Those entries are just the digit
values (0...9) for the corresponding images contained in the first
entry of the tuple.
The ``validation_data`` and ``test_data`` are similar, except
each contains only 10,000 images.
This is a nice data format, but for use in neural networks it's
helpful to modify the format of the ``training_data`` a little.
That's done in the wrapper function ``load_data_wrapper()``, see
below.
"""
f = gzip.open('../data/mnist.pkl.gz', 'rb')
training_data, validation_data, test_data = cPickle.load(f)
f.close()
return (training_data, validation_data, test_data)
def load_data_wrapper():
"""Return a tuple containing ``(training_data, validation_data,
test_data)``. Based on ``load_data``, but the format is more
convenient for use in our implementation of neural networks.
In particular, ``training_data`` is a list containing 50,000
2-tuples ``(x, y)``. ``x`` is a 784-dimensional numpy.ndarray
containing the input image. ``y`` is a 10-dimensional
numpy.ndarray representing the unit vector corresponding to the
correct digit for ``x``.
``validation_data`` and ``test_data`` are lists containing 10,000
2-tuples ``(x, y)``. In each case, ``x`` is a 784-dimensional
numpy.ndarry containing the input image, and ``y`` is the
corresponding classification, i.e., the digit values (integers)
corresponding to ``x``.
Obviously, this means we're using slightly different formats for
the training data and the validation / test data. These formats
turn out to be the most convenient for use in our neural network
code."""
tr_d, va_d, te_d = load_data()
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
training_results = [vectorized_result(y) for y in tr_d[1]]
training_data = zip(training_inputs, training_results)
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
validation_data = zip(validation_inputs, va_d[1])
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
test_data = zip(test_inputs, te_d[1])
return (training_data, validation_data, test_data)
def vectorized_result(j):
"""Return a 10-dimensional unit vector with a 1.0 in the jth
position and zeroes elsewhere. This is used to convert a digit
(0...9) into a corresponding desired output from the neural
network."""
e = np.zeros((10, 1))
e[j] = 1.0
return e
J'ai dit plus haut que nos programmes obtenaient de bons résultats. Qu'est-ce que cela signifie? Bons comparés à quoi? Il est instructif de disposer de quelques tests de référence simples (en dehors des réseaux de neurones) pour pouvoir faire des comparaisons et avoir une idée de ce qui peut être considéré comme des bons résultats. Le test de base le plus simple est bien sûr de deviner le chiffre au hasard. Le résultat sera correct dans dix pour cent des cas environ. Nous faisons beaucoup mieux que ça!
Essayons de trouver un test moins trivial, en utilisant une idée extrêmement simple: nous allons examiner à quelle point l'image est sombre. L'image d'un $2$ par exemple sera typiquement nettement plus sombre que l'image d'un $1$, simplement parce que davantage de pixels seront noirs, comme le montre l'exemple suivant:

Ceci suggère de calculer le niveau de noir moyen de chaque chiffre $0, 1, 2,\ldots, 9$ à partir des données d'entrainement. Lorsqu'une nouvelle image se présente, nous calculons son niveau moyen de noir, puis nous concluons qu'il s'agit du chiffre qui possède le niveau moyen de noir le plus proche. Il s'agit d'une procédure simple et facile à programmer, donc je n'écrirai pas explicitement le code - si cela vous intéresse, vous le trouverez dans le dépôt GitHub. Mais cette méthode est une nette amélioration par rapport à la méthode qui consiste à deviner au hasard, puisqu'elle obtient $2 225$ réponses correctes sur les $10 000$ images tests, c'est-à-dire une précision de $22,25$ pour cent.
Il n'est pas difficile de trouver d'autres idées qui atteignent des taux de réussite compris entre $20$ et $50$ pour cent. Si vous travaillez un peu plus dur, vous pouvez dépasser les $50$ pour cent. Mais pour obtenir de très bon taux de réussite, il est préférable d'utiliser les algorithmes d'apprentissage automatique qui ont fait leurs preuves. Essayons avec l'un des plus connus, la machine à vecteurs de support (support vector machine en anglais, abrégé en SVM). Si vous n'êtes pas familier avec les SVM, ne vous inquiétez pas, nous n'aurons pas besoin de comprendre leur fonctionnement en détail. Au lieu de cela, nous allons utiliser une bibliothèque Python appelée scikit-learn, qui fournit une interface Python simple avec une bibliothèque de fonctions rapides écrites en langage C, conçue pour les SVM, appelée LIBSVM.
Si nous exécutons le classifieur par SVM de scikit-learn, avec les paramètres par défaut, nous obtenons 9 435 réponses correctes sur 10 000 images tests. (le code est disponible ici.) C'est un énorme progrès par rapport à notre approche naïve de classification basée sur le niveau moyen de noir. En effet, cela signifie que la SVM obtient une performance presque équivalente à celle de nos réseaux de neurones, juste un tout petit peu moins bonne. Dans les prochains chapitres, nous introduirons de nouvelles techniques qui nous permettront d'améliorer nos réseaux de neurones, de sorte qu'ils fassent beaucoup mieux que les SVM.
Ce n'est pas la fin de l'histoire cependant. La performance de $9 435$ sur $10 000$ a été obtenue avec les paramètres par défaut pour les SVM de scikit-learn. Les SVM possèdent quelques paramètres réglables, et il est possible de chercher des paramètres qui améliorent cette performance brute. Je ne ferai pas cette recherche de façon explicite, vous pouvez vous référer à cet article de blog écrit par Andreas Mueller si vous voulez en savoir plus. Mueller montre qu'avec un travail sur l'optimisation des paramètres de la SVM, il est possible d'obtenir un taux de réussite qui dépasse 98,5 pour cent. Autrement dit, une SVM bien réglée ne commet qu'une erreur tous les 70 chiffres. C'est excellent! Est-ce que les réseaux de neurones peuvent faire mieux?
En fait, oui. A l'heure actuelle, des réseaux de neurones bien conçus surperforment toutes les autres techniques pour reconnaître les chiffres de MNIST, y compris les SVM. Le record actuel (en 2013) est de $9 979$ images correctement reconnues sur $10 000$. Il a été obtenu par Li Wan, Matthew Zeiler, Sixin Zhang, Yann LeCun, et Rob Fergus. Nous verrons plus loin dans le livre la plupart des techniques qu'ils ont utilisées. La performance obtenue est très proche de celle des humains, voire meilleure, étant donné que quelques images de MNIST sont difficiles à identifier avec certitude même pour des humains, comme par exemple:
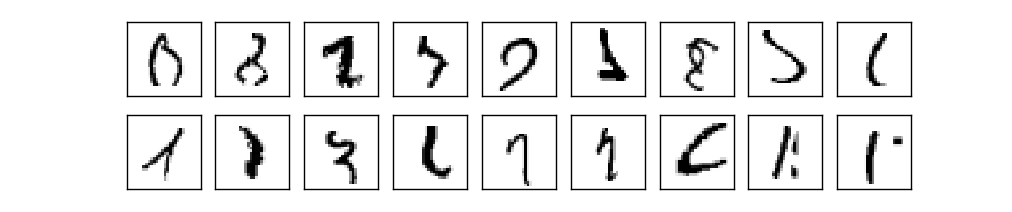
Je pense que vous serez d'accord que ces derniers sont difficiles à reconnaître! Avec des images telles que celles-ci dans la base de données MNIST, il est remarquable que des réseaux de neurones reconnaissent correctement toutes les images sauf 21 d'entre elles sur $10 000$ images de test. D'ordinaire, lorsqu'on programme, on pense que la résolution d'un problème compliqué tel que la reconnaissance des chiffres MNIST va nécessiter un algorithme sophistiqué. Mais même les réseaux de neurones de l'article de Wan et al mentionné précédemment ne mettent en jeu que des algorithmes tout à fait simples, qui sont des variantes de l'algorithme que nous avons vu dans ce chapitre. Toute la complexité est apprise automatiquement, à partir des données d'entrainement. En quelque sorte, la morale qu'il faut tirer de nos résultats et de ceux d'articles plus approfondis est que pour certains problèmes:
Vers l'apprentissage profond
Alors que nos réseaux de neurones donnent des performances impressionnantes, cette performance reste quelque peu mystérieuse. Les poids et les biais du réseau ont été découverts de façon automatique. Et cela implique que nous n'avons pas immédiatement d'explication concernant la façon dont le réseau agit. Pouvons-nous trouver un moyen de comprendre les principes selon lesquels notre réseau identifie les chiffres? Et à partir de ces principes, pouvons-nous faire mieux?
Pour poser ces questions de façon plus directe, supposons que d'ici quelques décennies, les réseaux de neurones mènent à l'intelligence artificielle (IA). Comprendrons-nous comment de tels réseaux intelligents fonctionnent? Peut-être que ces réseaux nous sembleront opaques, avec des poids et des biais que nous ne comprenons pas parce qu'ils ont été appris de manière automatique. Dans les débuts de l'IA, les chercheurs espéraient que les efforts pour construire une IA nous aideraient à comprendre les principes qui sont à la base de l'intelligence et peut-être aussi le fonctionnement du cerveau humain. Mais peut-être qu'au final, nous ne comprendrons ni le cerveau ni comment fonctionne l'intelligence artificielle!
Pour aborder ces questions, repensons à l'interprétation des neurones artificiels que j'ai donnée au début du chapitre, comme étant un moyen de soupeser les informations. Supposons que nous souhaitions déterminer si une image représente un visage ou non:
Sources: 1. Ester Inbar. 2. Inconnu. 3. NASA, ESA, G. Illingworth, D. Magee, et P. Oesch (Université de Californie, Santa Cruz), R. Bouwens (Université de Leiden), et l'équipe HUDF09. Cliquez sur les images pour plus de détails.
Nous pourrions aborder ce problème de la même façon que nous avons abordé la reconnaissance de caractères manuscrits - en utilisant les pixels de l'image comme entrées d'un réseau de neurones, avec comme sortie du réseau un unique neurone qui indique "Oui, c'est un visage" ou "Non ce n'est pas un visage".
Supposons que nous faisions cela, mais sans utiliser d'algorithme d'apprentissage. Au lieu de cela, nous allons essayer de concevoir un réseau à la main, en choisissant des poids et des biais appropriés. Comment pourrions-nous procéder? Si l'on oublie complètement les réseaux de neurones pour le moment, une méthode heuristique que nous pourrions employer serait de décomposer le problème en sous-problèmes: est-ce que l'image contient un oeil dans le coin supérieur gauche? Contient-elle un oeil dans le coin supérieur droit? Contient-elle un nez au milieu? Contient-elle une bouche en bas au milieu? Y a-t-il des cheveux en haut? Et ainsi de suite.
Si la réponse à plusieurs de ces questions est "oui", ou même seulement "probablement oui", alors nous pourrions conclure que l'image représente probablement un visage. Inversement, si la réponse à la plupart des questions est "non", alors l'image ne représente probablement pas un visage.
Evidemment, ceci n'est qu'une méthode heuristique grossière, et elle souffre de nombreux défauts. Peut-être que la personne est chauve et donc n'a pas de cheveux. Peut-être que nous ne voyons qu'une partie du visage, ou bien le visage est vu de profil ou une partie est ombragée. Cependant, cette méthode heuristique suggère que si nous sommes capables de résoudre les sous-problèmes avec des réseaux de neurones, alors peut-être que nous sommes capables de construire un réseau de neurones pour la détection de visages, en combinant les réseaux correspondant à chaque sous-problème. Voici une architecture possible, les rectangles représentant les sous-réseaux. Remarquez que le but n'est pas de donner une approche réaliste pour résoudre le problème de la détection de visages; il s'agit plutôt d'aider à se forger une intuition sur la façon dont les réseaux fonctionnent. Voici l'architecture:
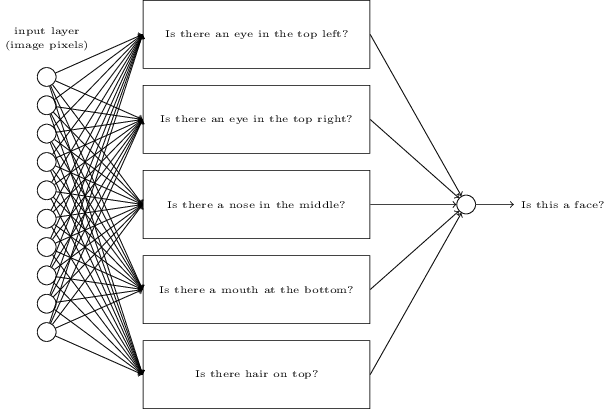
Il est également plausible que les sous-réseaux puissent être décomposés. Supposons que nous nous intéressions à la question: "Y a t-il un oeil dans le coin supérieur gauche?" Celle-ci peut être décomposée en questions telles que: "Y a-t-il un sourcil?"; "Y a-t-il des cils?"; "Y a-t-il un iris?"; et ainsi de suite. Bien sûr, ces questions devraient aussi porter sur de l'information positionnelle -"Est-ce que le sourcil est dans le coin supérieur gauche et au-dessus de l'iris?", mais restons simples. Le réseau qui répond à la question "Y a-t-il un oeil dans le coin supérieur gauche?" peut maintenant être décomposé:
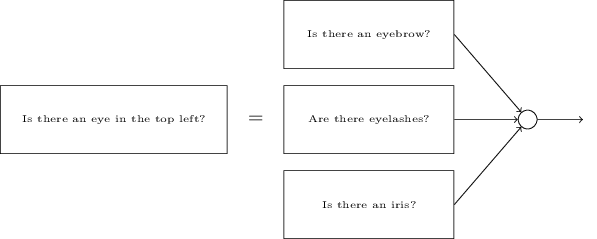
Ces questions aussi peuvent être réduites en miettes, toujours plus loin à travers les multiples couches. A la fin, nous travaillons avec des sous-réseaux qui répondent à des questions si simples que les réponses peuvent être obtenues au niveau des pixels individuels. Ces questions pourraient porter par exemple sur la présence ou l'absence de formes très simples en des points particuliers de l'image. De telles questions peuvent être traitées par des neurones uniques connectés aux pixels bruts de l'image.
Le résultat final est un réseau qui décompose une question très compliquée - est-ce que cette image représente ou non un visage? - en des questions très simples qui peuvent être traitées au niveau des pixels individuels. Le réseau effectue cela à travers une série de nombreuses couches, les premières couches répondant à des questions très simples et très spécifiques concernant l'image d'entrée, et les dernières couches construisant une hiérarchie de concepts toujours plus abstraits et complexes. Des réseaux qui possèdent ce genre de structure avec plusieurs couches - deux couches cachées ou plus - sont appelés des réseaux de neurones profonds.
Bien sûr, je n'ai pas expliqué comment réaliser cette décomposition récursive en sous-réseaux. Il est évidemment inconcevable de régler manuellement les poids et les biais du réseau. Au lieu de cela, nous aimerions utiliser des algorithmes d'apprentissage conçus pour que le réseau puisse apprendre de manière automatique les poids et les biais - et donc aussi la hiérarchie des concepts - à partir des données d'entrainement. Les chercheurs des années 80 et 90 ont essayé d'utiliser la descente de gradient stochastique et la rétropropagation pour entrainer des réseaux profonds. Malheureusement, à part pour quelques architectures spécifiques, ils n'ont pas connu beaucoup de réussite. Les réseaux apprenaient, mais très lentement, et souvent trop lentement pour être utiles en pratique.
Depuis 2003, toute une gamme de techniques ont été développées pour permettre l'apprentissage avec les réseaux de neurones profonds. Ces techniques d'apprentissage profond sont basées sur la descente de gradient stochastique et la rétropropagation, mais elles introduisent aussi de nouvelles idées. Ces techniques ont permis à des réseaux beaucoup plus profonds (et plus larges) d'être entrainés - il est maintenant courant d'entrainer des réseaux avec 5 à 10 couches cachées. Et il s'avère que, pour de nombreux problèmes, ces derniers ont des performances bien meilleures que les réseaux de neurones peu profonds, c'est-à-dire des réseaux avec une unique couche cachée. La raison de ce succès est bien sûr la capacité des réseaux profonds à construire une hiérarchie complexe de concepts. Cela ressemble un peu à la façon dont les langages de programmation conventionnels utilisent une conception par modules et par objet pour permettre la création de programmes informatiques complexes. Comparer un réseau profond à un réseau peu profond est un peu comme comparer un langage de programmation capable d'effectuer des appels de fonctions à un langage dépouillé et incapable de faire cela. Par rapport à la programmation conventionnelle, l'abstraction prend une forme différente dans le cas des réseaux de neurones mais elle est tout aussi importante.